Как будет «граничная скорость» по-английски? перевод слова «граничная скорость»

Равномерное движение по прямой линии

Это идеализированный тип движения, который предполагает, что тело в течение некоторого промежутка времени движется вдоль прямой в пространстве. При этом скорость тела не меняется. Обозначая пройденный путь символом l, получаем формулу:

l = v*t.

Здесь v = const.

Этот тип движения рассматривался еще философами Античной Греции. Они полагали, что для движения тел необходимо прикладывать некоторую силу, поэтому естественным состоянием всех окружающих объектов является покой. Только с приходом эпохи Возрождения благодаря работам Галилея и Ньютона было показано, что если на тело не воздействуют внешние силы, то равномерность и прямолинейность его движения не нарушается.

Некоторые скорости

Космические скорости

Анализ первой и второй космической скорости по Исааку Ньютону. Снаряды A и B падают на Землю. Снаряд C выходит на круговую орбиту, D — на эллиптическую. Снаряд E улетает в открытый космос

Небесная механика изучает поведение тел Солнечной системы и других небесных тел. Движение искусственных космических тел изучается в астродинамике. При этом рассматривается несколько вариантов движения тел, для каждого из которых необходимо придание определённой скорости. Для вывода спутника на круговую орбиту ему необходимо придать первую космическую скорость (например, искусственный спутник Земли); преодолеть гравитационное притяжение позволит вторая космическая скорость (например, объект запущенный с Земли, вышедший за её орбиту, но находящийся в Солнечной системе); третья космическая скорость нужна чтобы покинуть звёздную систему, преодолев притяжение звезды (например, объект запущенный с Земли, вышедший за её орбиту и за пределы Солнечной системы); четвёртая космическая скорость позволит покинуть галактику.

В небесной механике под орбитальной скоростью понимают скорость вращения тела вокруг барицентра системы.

Скорость звука

Основная статья: Скорость звука

Скорость звука — скорость распространения упругих волн в среде, определяется упругостью и плотностью среды. Скорость звука не является постоянной величиной и зависит от температуры (в газах), от направления распространения волны (в монокристаллах). При заданных внешних условиях обычно не зависит от частоты волны и её амплитуды. В тех случаях, когда это не выполняется и скорость звука зависит от частоты, говорят о дисперсии звука. Впервые измерена Уильямом Дерхамом. Как правило, в газах скорость звука меньше, чем в жидкостях, а в жидкостях скорость звука меньше, чем в твёрдых телах, поэтому при сжижении газа скорость звука возрастает.

Отношение скорости течения в данной точке газового потока к местной скорости распространения звука в движущейся среде называется числом Маха по имени австрийского учёного Эрнста Маха. Упрощённо, скорость, соответствующая 1 Маху при давлении в 1 атм (у земли на уровне моря), будет равна скорости звука в воздухе. Движение аппаратов со скоростью, сравнимой со скоростью звука, сопровождается рядом явлений, которые называются звуковой барьер. Скорости от 1,2 до 5 Махов называются сверхзвуковыми, скорости выше 5 Махов — гиперзвуковыми.

Скорость света

Основная статья: Скорость света

Время распространения светового луча в масштабной модели Земля-Луна. Для преодоления расстояния от поверхности Земли до поверхности Луны свету требуется 1,255 секунды.

Скорость света в вакууме — абсолютная величина скорости распространения электромагнитных волн в вакууме. Традиционно обозначается латинской буквой «c» (произносится как ). Скорость света в вакууме — фундаментальная постоянная, не зависящая от выбора инерциальной системы отсчёта (ИСО). Она относится к фундаментальным физическим постоянным, которые характеризуют не просто отдельные тела или поля, а свойства пространства-времени в целом. По современным представлениям, скорость света в вакууме — предельная скорость движения частиц и распространения взаимодействий.

Наиболее точное измерение скорости света 299 792 458 ± 1,2 м/с на основе эталонного метра было проведено в 1975 году. Теперь ввиду современного определения метра скорость света считается равной точно 299792458 м/с.

Скорость гравитации

Основная статья: Скорость гравитации

Скорость гравитации — скорость распространения гравитационных воздействий, возмущений и волн. До сих пор остаётся не определённой экспериментально, но согласно общей теории относительности должна совпадать со скоростью света.

Структурно-функциональная организация кровеносной системы. Функциональная роль амортизирующих, резистивных, обменных и емкостных сосудов

Подробности

Различные участки кровеносного русла имеют различные характеристики. Это позволяет участкам сосудистого русла выполнять функции амортизирующих, резистивных, обменных и емкостных сосудов.

Объемная скорость кровотока

Объемная скорость кровотока (Q)— это количество крови, которое проходит через определенное суммарное сечение сосудов в единицу времени (обычно за одну минуту). Суммарный просвет сосудов постепенно увеличивается, включая капилляры, где он максимальный, а затем постепенно уменьшается. Однако, в полых венах он в 1,5-2 раза больше, чем в аорте.

Объемную скорость можно определить по формуле:

Q = (P1-P2) / W.

Иначе, объемная скорость (Q) равняется разности давлений крови в начальной и конечной части сосудистой системы (P1-P2), поделенной на сопротивление этого отдела сосудистой системы (W).

Отсюда, чем больше разность давлений крови, и чем меньше сопротивление, тем больше объемная скорость. Однако, эту формулу для определения объемной скорости можно использовать только теоретически.

Объемная скорость во всех суммарных сечениях сосудов одинакова и составляет у взрослого и здорового человека в состоянии покоя в среднем 4-5 литров крови за минуту.

Однако, это совсем не означает, что в различных участках одного сечения она одинакова, то есть в одном участке этого сечения она увеличивается (площадь поперечного сечения здесь соответственно уменьшается), то в других она соответственно уменьшается (следовательно, площадь поперечного сечения здесь возрастает). На этом основано перераспределение кровообращения в зависимости от функциональной нагрузки. Объемную скорость кровообращения за 1 минуту иначе можно назвать минутным объемом кровообращения (МОК). При физическом напряжении минутный объем кровообращения (МОК) увеличивается и может доходить до 30 литров крови. Если учесть, что объемная скорость и МОК — одна и та же величина, то практически для ее определения можно использовать все методы, которые применяются для оценки МОК, а именно методы Фика, индикаторный, Грольмана и др., о которых шла речь в подразделе “Физиология сердца”.

Линейная скорость кровотока

Линейная скорость кровотока (V) оценивается расстоянием, которое проходит частица крови в единицу времени (секунда). Ее легко можно вычислить по формуле:

V = Q / P*r2

где Q — объемная скорость, (P*r2) — сечение сосуда (имеется в виду суммарный просвет сосудов соответствующего калибра). Как следует из формулы, линейная скорость находится в прямой зависимости от объемной скорости, и обратной зависимости — от сечения сосудов.

Отсюда следует, что линейная скорость должна быть различной в разных сечениях сосудов. Так в состоянии покоя линейная скорость в аорте составляет 400-600 мм/с, в артериях среднего калибра — 200-300 мм/с, в артериолах — 8-10 мм/с, в капиллярах — 0,3-0,5 мм/с. Затем по ходу венозного кровотока линейная скорость постепенно возрастает, т. к.

суммарный просвет сосудов уменьшается и в полых венах она доходит до 150-200 мм/с.

Кроме того, в начальной части аорты она может уменьшаться или даже быть нулевой, т. к. при падении давления в левом желудочке, кровь естественно устремляется по направлению к сердечной мышце в силу разности давлений.

При физической нагрузке линейная скорость увеличивается во всех сечениях сосудистой системы.

Определение	Артерии	Капилляры	Вены
Строение	Стенки аорты состоят преимущественно из эластических волокон	В состав стенок других артерий входят также и мышечные элементы, что делает возможным процесс нейрогуморальной регуляции их просвета	Стенка капилляра представляет собой слой эндотелиальных клеток, расположенных на базальной мембране	– В венах имеются клапаны – В стенках вен присутствуют как эластические, так и мышечные волокна
Функция	Часть энергии систолы передается на стенки этих сосудов. Под давлением крови стенки растягиваются и за счет сокращений проталкивают кровь дальше по направлению к периферии	Объем кровотока в тканях корригируется «по потребности». Просвет артериальных сосудов может меняться, что, несомненно, сказывается на системном артериальном давлении	Питательные вещества и кислород диффундируют в ткани, а продукты клеточного метаболизма, в том числе и углекислый газ в кровеносное русло	– Обеспечивают ток крови только в одном направлении – Регулируют объем циркулирующей крови

Аорта и крупные артерии	Амортизирующие (проводящие, распределительные) сосуды
Мелкие артерии и артериолы	Сосуды сопротивления (резистивные сосуды), регулируют кровоснабжение тканей и уровень артериального давления
Капилляры	Обменные сосуды
Венулы и вены	Ёмкостные сосуды

Измерения ускорений

Используемые единицы

• метр на секунду в квадрате (метр в секунду за секунду), м/с², производная единица системы СИ;
• сантиметр на секунду в квадрате (сантиметр в секунду за секунду), см/с², производная единица системы СГС, имеет также собственное наименование гал, или галилео (применяется преимущественно в гравиметрии);
• g (произносится «же»), стандартное ускорение свободного падения на поверхности Земли, равное по определению 9,80665 м/с². В технических расчётах, не требующих точности выше 2 %, часто используется приближение g ≈ 10 м/с².

Преобразования между различными единицами ускорения

	м/с2	фут/с2	g	см/с2
1 м/с2 =	1	3,28084	0,101972	100
1 фут/с2 =	0,304800	1	0,0310810	30,4800
1 g =	9,80665	32,1740	1	980,665
1 см/с2 =	0,01	0,0328084	0,00101972	1

Технические средства

Приборы для измерения ускорения называются акселерометрами. Они не «детектируют» ускорение непосредственно, а измеряют силу реакции (укр.)русск. опоры, возникающую при ускоренном движении. Поскольку аналогичные силы сопротивления возникают в поле тяготения, с помощью акселерометров можно измерять также гравитацию.

Акселерографы — приборы, измеряющие и автоматически записывающие (в виде графиков) значения ускорения поступательного и вращательного движения.

Значения ускорения в некоторых случаях

Значения ускорений различных движений:

Вид движения	Ускорение, м/с2
Центростремительное ускорение Солнечной системы при орбитальном движении в Галактике	2,2⋅10−10
Центростремительное ускорение Земли при орбитальном движении вокруг Солнца	0,0060
Центростремительное ускорение Луны при орбитальном движении вокруг Земли	0,0027
Пассажирский лифт	0,9—1,6
Поезд метро	1
Автомобиль «Жигули»	1,5
Бегун на коротких дистанциях	1,5
Велосипедист	1,7
Конькобежец	1,9
Мотоцикл	3—6
Аварийное торможение автомобиля	4—6
Усэйн Болт, максимальное ускорение	8
Гоночный автомобиль	8—9
Торможение при открытии парашюта	30 (3 g)
Запуск и торможение космического корабля	40—60 (4—6 g)
Манёвр реактивного самолёта	до 100 (до 10 g)
Свая после удара копром	300 (30 g)
Поршень двигателя внутреннего сгорания	3×103
Пуля в стволе винтовки	2,5×105
Микрочастицы в ускорителе	(2—50)×1014
Электроны между катодом и анодом трубки цветного телевизора (20 кВ, 0,5 м)	≈7×1015
Электроны при соударении с люминофором трубки цветного телевизора (20 кВ)	≈1022
Альфа-частицы в атомном ядре	≈1027

Примечание: здесь g ≈ 10 м/с2.

Создание ускорения. Динамика точки

Первый закон Ньютона постулирует существование инерциальных систем отсчёта. В этих системах отсчёта равномерное прямолинейное движение имеет место в том случае, когда тело (материальная точка) не подвергается никаким внешним воздействиям в процессе своего движения. На основе этого закона возникает ключевое для механики понятие силы как такого внешнего воздействия на тело, которое выводит его из состояния покоя или влияет на скорость его движения. Таким образом, постулируется, что причиной возникновения ненулевого ускорения в инерциальной системе отсчёта всегда является некоторое внешнее силовое воздействие.

Классическая механика

Второй закон Ньютона применительно к нерелятивистскому движению (то есть к движению со скоростями, много меньшими скорости света) утверждает, что ускорение материальной точки всегда пропорционально приложенной к ней и порождающей ускорение силе, причём коэффициент пропорциональности всегда один и тот же независимо от вида силового воздействия (он называется инертной массой материальной точки):

ma→=F→.{\displaystyle m{\vec {a}}={\vec {F}}.}

Если известны масса материальной точки и (как функция времени) сила, действующая на неё, то из второго закона Ньютона известно и её ускорение: a→=F→m.{\displaystyle {\vec {a}}={\vec {F}}/m.} При постоянстве силы ускорение также будет постоянным. Скорость и координаты точки в любой момент времени можно получить, проинтегрировав ускорение по формулам из раздела о кинематике точки при заданных начальных скорости и координатах.

Релятивистская механика

Основная статья: Релятивистски равноускоренное движение

В релятивистской физике второй закон Ньютона записывается в форме

mddtv→1−v2c2=F→{\displaystyle m{\frac {d}{dt}}{\frac {\vec {v}}{\sqrt {1-v^{2}/c^{2}}}}={\vec {F}}}

что делает нахождение ускорения более сложной задачей, чем в классическом случае. В частности, длительное движение с постоянным ускорением принципиально невозможно (иначе скорость точки в конце концов превысит скорость света), а неизменность силы не означает неизменности ускорения: оно будет стремиться к нулю при нарастании скорости. Тем не менее, если зависимость a→(t){\displaystyle {\vec {a}}(t)} всё же найдена, расчёт v→(t){\displaystyle {\vec {v}}(t)} и r→(t){\displaystyle {\vec {r}}(t)} осуществим по тем же формулам, что и в нерелятивистском пределе.

Связанные понятия

Ряд понятий классической механики выражаются через скорость.

Импульс, или количество движения, — это мера механического движения точки, которая определяется как произведение массы точки на его скорость p→=mv→{\displaystyle {\vec {p}}=m{\vec {v}}}. Импульс является векторной величиной, его направление совпадает с направлением скорости. Для замкнутой системы выполняется закон сохранения импульса. Обобщением импульса в релятивистских системах является четырёхимпульс, временная компонента которого равна Ec{\displaystyle E/c}. Для обобщённого импульса также выполняется равенство:

pμ=mUμ,{\displaystyle p^{\mu }=m\,U^{\mu }\!,}

где Uμ{\displaystyle U^{\mu }} — обобщённая четырёхмерная скорость.

От скорости также зависит кинетическая энергия механической системы. Для абсолютно твёрдого тела полную кинетическую энергию можно записать в виде суммы кинетической энергии поступательного и вращательного движения:

T=mv22+Iω→22,{\displaystyle T={\frac {mv^{2}}{2}}+{\frac {{\mathcal {I}}{\vec {\omega }}^{2}}{2}},}

где  m{\displaystyle \ m} — масса тела,  v{\displaystyle \ v} — скорость центра масс тела, I{\displaystyle {\mathcal {I}}} — момент инерции тела, ω→{\displaystyle {\vec {\omega }}} — угловая скорость тела.

Изменение скорости по времени характеризуется ускорением. Ускорение отражает изменение скорости как по величине (тангенциальное ускорение), так и по направлению (центростремительное ускорение):

a→=dv→dt=a→τ+a→n=d|v→|dte→τ+v2re→n,{\displaystyle {\vec {a}}={\frac {\mathrm {d} {\vec {v}}}{\mathrm {d} t}}={\vec {a}}_{\tau }+{\vec {a}}_{n}={\frac {\mathrm {d} |{\vec {v}}|}{\mathrm {d} t}}{\vec {e}}_{\tau }+{v^{2} \over r}{\vec {e}}_{n},}

где  r{\displaystyle \ r} — радиус кривизны траектории точки.

В релятивистской механике угол между касательной к мировой линии частицы и осью времени в базовой системе отсчёта носит название быстроты (обозначается θ{\displaystyle \theta }). Быстрота выражается формулой:

θ=cArthvc=c2ln⁡1+vc1−vc,{\displaystyle \theta =c\,\mathrm {Arth} \,{\frac {v}{c}}={\frac {c}{2}}\ln {\frac {1+{\dfrac {v}{c}}}{1-{\dfrac {v}{c}}}},}

где Arthx{\displaystyle \mathrm {Arth} \,x} — ареатангенс, или гиперболический арктангенс. Быстрота стремится к бесконечности когда скорость стремится к скорости света. В отличие от скорости, для которой необходимо пользоваться преобразованиями Лоренца, быстрота аддитивна, то есть

θ′=θ+θ,{\displaystyle \theta ‘=\theta +\theta _{0},}

где θ{\displaystyle \theta _{0}} — быстрота системы отсчёта S′{\displaystyle S’} относительно системы отсчёта S{\displaystyle S}.

Интерпретация поверхностных волн

Применяется как вспомогательный метод для уточнения границы минерального дна или толщины
насыпи.

При интерпретации поверхностных поперечных волн для определения толщины слоя болотной залежи или толщины земляного полотна на болоте обычно имеем два случая: а) поверхностный слой расположен на слое с большей скоростью распространения поперечных волн SH;
б) поверхностный слой расположен на слое с меньшей скоростью распространения SH.

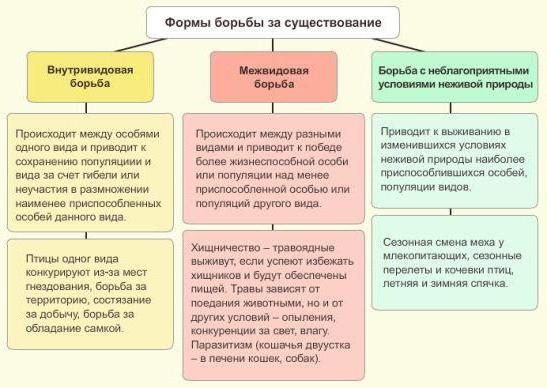
В первом случае
используют формулу //

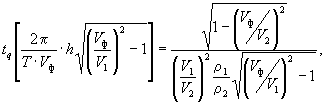
где T — квазипериод;

V_ф—
фазовая скорость;

V₂ — скорость во втором слое.

Во втором случае для определения толщины насыпи (поверхностный слой) на болоте используют формулы /, /, справедливые в том случае, когда подстилающий слой по своим свойствам близок к жидкости:

 

где V_гр — групповая
скорость.

Простейший способ определения фазовой скорости состоит в том, что определяют разность времен (t₀₂ — t₀₁) появления
одной и той же фазы, М₁ и М₂ на сейсмограмме. На эту
разность делят разность расстояний (X₂ — X₁) между сейсмоприемниками (рис. ).

Рис. 17. Схема определения фазовой скорости

Групповая скорость
— скорость
движения всей группы волн (волнового пакета, цуга), определяемая по движению середины всей группы волн.

Точность определения глубины и толщины насыпи поверхностными волнами ниже, чем
преломленными. Погрешность этого метода составляет 10 — 20 % по сравнению с бурением.

Понятие «обобщённое ускорение»

Если динамика механической системы описывается не в декартовых, а в обобщённых координатах qi{\displaystyle q_{i}} (например, в гамильтоновой или в лагранжевой формулировках механики), то можно ввести обобщённые ускорения qi¨{\displaystyle {\ddot {q_{i}}}} — первые производные по времени обобщённых скоростей qi˙{\displaystyle {\dot {q_{i}}}} или вторые производные по времени обобщённых координат; например, если в качестве одной из обобщённых координат выбран угол, то обобщённым ускорением будет соответствующее угловое ускорение. Размерность обобщённых ускорений в общем случае не равна LT−2.

Движение тела по окружности с постоянной по модулю скоростью

Движение тела по окружности с постоянной по модулю скоростью — это движение, при котором тело за любые равные промежутки времени описывает одинаковые дуги.

Положение тела на окружности определяется радиусом-вектором \(~\vec r\), проведенным из центра окружности. Модуль радиуса-вектора равен радиусу окружности R (рис. 1).

Рис. 1

За время Δt тело, двигаясь из точки А в точку В, совершает перемещение \(~\Delta \vec r\), равное хорде АВ, и проходит путь, равный длине дуги l.

Радиус-вектор поворачивается на угол Δφ. Угол выражают в радианах.

Скорость \(~\vec \upsilon\) движения тела по траектории (окружности) направлена по касательной к траектории. Она называется линейной скоростью. Модуль линейной скорости равен отношению длины дуги окружности l к промежутку времени Δt за который эта дуга пройдена:

\(~\upsilon = \frac{l}{\Delta t}.\)

Скалярная физическая величина, численно равная отношению угла поворота радиуса-вектора к промежутку времени, за который этот поворот произошел, называется угловой скоростью:

\(~\omega = \frac{\Delta \varphi}{\Delta t}.\)

В СИ единицей угловой скорости является радиан в секунду (рад/с).

При равномерном движении по окружности угловая скорость и модуль линейной скорости — величины постоянные: ω = const; υ = const.

Положение тела можно определить, если известен модуль радиуса-вектора \(~\vec r\) и угол φ, который он составляет с осью Ox (угловая координата). Если в начальный момент времени t = 0 угловая координата равна φ, а в момент времени t она равна φ, то угол поворота Δφ радиуса-вектора за время \(~\Delta t = t — t_0 = t\) равен \(~\Delta \varphi = \varphi — \varphi_0\). Тогда из последней формулы можно получить кинематическое уравнение движения материальной точки по окружности:

\(~\varphi = \varphi_0 + \omega t.\)

Оно позволяет определить положение тела в любой момент времени t. Учитывая, что \(~\Delta \varphi = \frac{l}{R}\), получаем\

\(~\upsilon = \omega R\) — формула связи между линейной и угловой скоростью.

Промежуток времени Τ, в течение которого тело совершает один полный оборот, называется периодом вращения:

\(~T = \frac{\Delta t}{N},\)

где N — число оборотов, совершенных телом за время Δt.

За время Δt = Τ тело проходит путь \(~l = 2 \pi R\). Следовательно,

\(~\upsilon = \frac{2 \pi R}{T}; \ \omega = \frac{2 \pi}{T} .\)

Величина ν, обратная периоду, показывающая, сколько оборотов совершает тело за единицу времени, называется частотой вращения:

\(~\nu = \frac{1}{T} = \frac{N}{\Delta t}.\)

Следовательно,

\(~\upsilon = 2 \pi \nu R; \ \omega = 2 \pi \nu .\)

Задача на определения линейной скорости нашей планеты

Каждый человек понимает, что если автомобиль движется со скоростью 100 км/ч, то эта цифра является достаточно большой в сравнении со скоростями, с которыми люди сталкиваются в повседневной жизни. Любопытно сравнить указанную цифру со скоростью вращения Земли по своей орбите.

Для оценки этой скорости возьмем следующие данные:

• радиус орбиты — 150 млн км;
• период одного оборота — 365 земных дней.

Для определения требуемой величины воспользуемся формулой линейной и угловой скорости:

v = ω*r.

Значение ω через период T определяется так:

ω = 2*pi/T.

Тогда для v приходим к равенству:

v = 2*pi*r/T.

Подставляя данные из условия задачи, получим линейную скорость 107,5 тысяч км/ч! Эта цифра означает, что наша Земля перемещается в космическом пространстве в 1000 раз быстрее, чем автомобиль движется по дороге. Мы не чувствуем этой гигантскую скорости, поскольку силы гравитации Земли увлекают за собой атмосферу так, что она находится в покое относительно поверхности планеты.

Угловая скорость в спорте

Угловая скорость часто используется в спорте. Например, спортсмены уменьшают или увеличивают угловую скорость движения клюшки для гольфа, биты или ракетки, чтобы улучшить результаты. Угловая скорость связана с линейной скоростью так, что из всех точек на отрезке, вращающемся вокруг точки на этом отрезке, то есть вокруг центра вращения, самая отдаленная точка от этого центра движется с самой высокой линейной скоростью. Так, например, если клюшка для гольфа вращается, то конец этой клюшки, больше всего удаленный от центра вращения двигается с самой высокой линейной скоростью. В то же время все точки на этом отрезке движутся с одинаковой угловой скоростью. Поэтому удлиняя клюшку, биту, или ракетку, спортсмен также увеличивает линейную скорость, а соответственно скорость удара, передающуюся мячу, так что он может пролететь на большее расстояние. Укорачивая ракетку или клюшку, даже перехватив ее ниже, чем обычно, наоборот замедляют скорость удара.

При первобытнообщинном строе главными охотниками были мужчины

Спортсменам с более длинными руками и ногами удается добиться бо́льшей угловой скорости

У высоких людей с длинными конечностями есть преимущество в отношении линейной скорости. То есть, передвигая ноги с одинаковой угловой скоростью, они двигают ступни с более высокой линейной скоростью. То же происходит и с их руками. Такое преимущество может быть одной из причин того, что в первобытных обществах мужчины занимались охотой чаще, чем женщины. Вероятно, что из-за этого также в процессе эволюции выиграли более высокие люди. Длинные конечности помогали не только в беге, но и во время охоты — длинные руки бросали копья и камни с большей линейной скоростью. С другой стороны, длинные руки и ноги могут быть неудобством. Длинные конечности имеют больший вес и для их перемещения нужна дополнительная энергия. Кроме этого, когда человек быстро бежит, длинные ноги быстрее двигаются, а значит, при столкновении с препятствием удар будет сильнее, чем у людей с короткими ногами, которые двигаются с той же линейной скоростью.

В гимнастике, фигурном катании и нырянии также используют угловую скорость. Если спортсмен знает угловую скорость, то легко вычислить количество переворотов и других акробатических трюков во время прыжка. Во время кувырков спортсмены обычно прижимают ноги и руки как можно ближе к корпусу, чтобы уменьшить инерцию и увеличить ускорение, а значит и угловую скорость. С другой стороны, во время ныряния или приземления, судьи смотрят, как ровно спортсмен приземлился. На высокой скорости трудно регулировать направление полета, поэтому спортсмены специально замедляют угловую скорость, немного вытягивая от корпуса руки и ноги.

Спортсмены, которые занимаются метанием диска или молота, тоже контролируют линейную скорость с помощью угловой. Если просто бросить молот, не вращая его по кругу на длинной стальной проволоке, увеличивающей линейную скорость, то бросок будет не таким сильным, поэтому молот сначала раскручивают. Олимпийские спортсмены поворачиваются вокруг своей оси от трех до четырех раз, чтобы увеличить угловую скорость до максимально возможной.

Угловая скорость

Когда тело движется по окружности, то не все его точки движутся с одинаковой скоростью относительно оси вращения. Если взять лопасти обычного бытового вентилятора, которые вращаются вокруг вала, то точка расположенная ближе к валу имеет скорость вращения больше, чем отмеченная точка на краю лопасти. Это значит, у них разная линейная скорость вращения. В то же время угловая скорость у всех точек одинаковая.

Угловая скорость представляет собой изменение угла в единицу времени, а не расстояния. Обозначается буквой греческого алфавита – ω и имеет единицу измерения радиан в секунду (рад/с). Иными словами, угловая скорость – это вектор, привязанный к оси обращения предмета.

Формула для вычисления отношения между углом поворота и временным интервалом выглядит так:

ω = ∆ϕ/∆t,

где:

• ω – угловая скорость (рад./с);
• ∆ϕ – изменение угла отклонения при повороте (рад.);
• ∆t – время, затраченное на отклонение (с).

Обозначение угловой скорости употребляется при изучении законов вращения. Оно употребляется при описании движения всех вращающихся тел.

Формула угловой скорости

Угловая скорость в конкретных случаях

На практике редко работают с величинами угловой скорости. Она нужна при конструкторских разработках вращающихся механизмов: редукторов, коробок передач и прочего.

Вычислить её, применяя формулу, можно. Для этого используют связь угловой скорости и частоты вращения.

ω = 2*π / Т = 2*π*ν,

где:

• π – число, равное 3,14;
• ν – частота вращения, (об./мин.).

В качестве примера могут быть рассмотрены угловая скорость и частота вращения колёсного диска при движении мотоблока. Часто необходимо уменьшить или увеличить скорость механизма. Для этого применяют устройство в виде редуктора, при помощи которого понижают скорость вращения колёс. При максимальной скорости движения 10 км/ч колесо делает около 60 об./мин. После перевода минут в секунды это значение равно 1 об./с. После подстановки данных в формулу получится результат:

ω = 2*π*ν = 2*3,14*1 = 6,28 рад./с.

К сведению. Снижение угловой скорости часто требуется для того, чтобы увеличить крутящий момент или тяговое усилие механизмов.

Шестерёнчатый уменьшитель хода для мотокультиватора

Как определить угловую скорость

Принцип определения угловой скорости зависит от того, как происходит движение по окружности. Если равномерно, то употребляется формула:

ω = 2*π*ν.

Если нет, то придётся высчитывать значения мгновенной или средней угловой скорости.

Величина, о которой идёт разговор, векторная, и при определении её направления используют правило Максвелла. В просторечии – правило буравчика. Вектор скорости имеет одинаковое направление с поступательным перемещением винта, имеющего правую резьбу.

Правило Максвелла для угловой скорости

Рассмотрим на примере, как определить угловую скорость, зная, что угол поворота диска радиусом 0,5 м меняется по закону ϕ = 6*t:

ω = ϕ / t = 6 * t / t = 6 с-1

Вектор ω меняется из-за поворота в пространстве оси вращения и при изменении значения модуля угловой скорости.

Построение преломляющих границ

Глубины преломляющих границ
можно определить двумя способами: менее точным, но более быстрым
способом средних скоростей () и более точным, но более громоздким способом пластовых скоростей (V_п). Оба эти способа являются упрощенными модификациями
точного способа
полей времени /

При простом строении (двухслойная среда, горизонтальная граница) залежи можно применять и другие упрощенные способы, основанные на ряде
допущений /

Способ средних скоростей /, ,

Все слои, лежащие выше искомых преломленных границ,
рассматривают как один однородный слой с постоянной скоростью распространения упругих волн. Для
построения границ необходимо иметь значения V_г,  и t.

V_г находят по одному из способов, описанных выше;  — по перегибу
годографа (точка пересечения прямой и
преломленной волны) и t— продолжением годографа
преломленной волны на ось времени (рис. а).

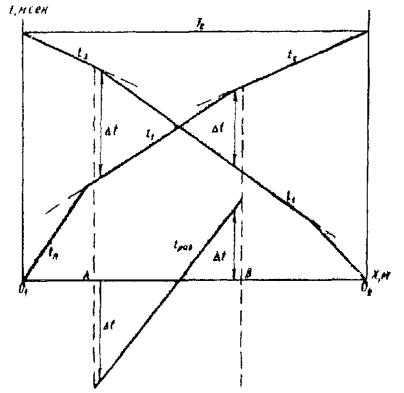
Рис. 11. Построение разностного годографа t_раз (для волны t₁) в случае неувязанной системы годографов

Для n-го слоя границу находят по формуле

где — средняя скорость до n-й границы;

V_г.п — граничная скорость вдоль этой границы;

t_n — значение t для n-й
границы.

Для первой границы раздела

Для первой границы можно использовать
также формулу

где X_т.п — точка пересечения
годографа прямой и преломленной волны.

Приближенно глубину можно определить (горизонтальная граница,
двухслойная среда) по положению точки перегиба (X_т.п), как h = (0,33 ÷
0,4)·X_т.п

Если имеется систем встречных годографов, увязанных во взаимных точках, то глубину залежи в любой точке профиля (имеющего перекрытый участок) можно определить по построенной линии t_0(X), которую находит из соотношения

Построение показано на рис. б.

Рис.
12. Определение средних скоростей и t для многослойного разреза (а) и построение
линий t(X) при встречной системе с перекрытыми участками (б)

Способ пластовых скоростей /, ,

Для определения мощности каждого слоя необходимо знать t
и
V_г для каждой границы.

Мощность первого слоя определяют способом, описанным выше.

Мощность второго слоя

гдеi₁₂ = arcsin(V₁V_г.1); i₁₃ = arcsin(V₁V_г.2); i₂₃ = arcsin(V_г.1V_г.2).

Мощность третьего слоя

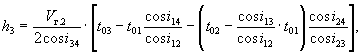
гдеi₁₄ = arcsin(V₁V_г.3); i₂₄ = arcsin(V_г.1V_г.3); i₃₄ = arcsin(V_г.2V_г.3);

t₀₁, t₀₂, t₀₃ — соответственно время, отсекаемое на оси времен продолжениями
первого, второго и последнего отрезков годографов преломленных волн.

Аналогичные формулы выводят и для следующих слоев.

Глубины преломляющих границ находят суммированием мощностей залегающих выше слоев.

Для приближенного определения V_г.iв методе пластовых скоростей можно использовать формулу /

где  и  — кажущиеся скорости преломленных волн от одной и той же границы, зарегистрированные по подъему и падению
ее.

При использовании одноканальных установок (при двухслойной среде) целесообразно определять положение наклонной границы по годографам из одной точки пункта возбуждения по
способу расстояний (рис. )

Наклон границы
определяют по формуле

где

 

а ее глубину — по формуле  или как показано на рис. .

 

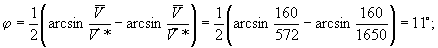
Рис. 13. Определение угла наклона
и глубины залежи из одной точки пункта возбуждения

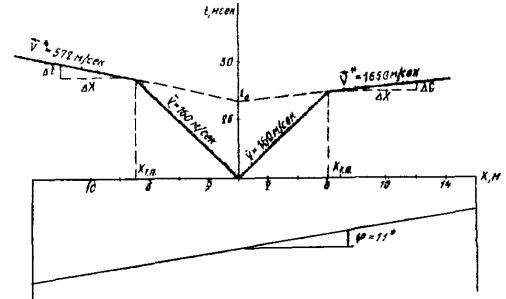
Рис. 14. Упрощенный аналитический способ определения скоростей и глубины залежи с центральным пунктом возбуждения

Линейные и угловые величины

Как уже говорилось, нам надо ввести такие физические величины, которые характеризовали бы неравномерное вращение колеса (в системе отсчета, связанной с троллейбусом). Попробуем это сделать по аналогии с прямолинейным неравномерным движением.

Проследим за точкой М колеса в течение малого промежутка времени Δt. За это время точка пройдет по дуге окружности путь s и будет иметь скорость υ и касательное ускорение a_k (рис. 2). Три величины s, υ и a_k, называемые линейными величинами, характеризуют движение точки М, но не могут служить для описания вращения всего колеса, так как в один и тот же момент времени другие точки, расположенные на других расстояниях от оси вращения, имеют другие линейные скорости, и касательные ускорения и пройденные ими пути тоже не одинаковы. Поэтому кроме линейных вводятся так называемые угловые величины, которые одинаковы для всех точек вращающегося колеса: угол поворота φ радиуса, соединяющего точку М с центром окружности, угловая скорость \(~\omega = \frac{\Delta \varphi}{\Delta t}\) (Δφ — изменение угла поворота за время Δt) и угловое ускорение \(~\varepsilon = \frac{\Delta \omega}{\Delta t}\) (Δω — изменение угловой скорости).

Рис. 2

Очевидно, что введенными здесь угловыми величинами можно описывать вращение не только троллейбусного колеса, но и любого другого тела. При этом с течением времени может изменяться не только угол поворота φ, но и угловая скорость ω и угловое ускорение ε. В частности, если угловое ускорение не зависит от времени, то угловая скорость изменяется равномерно и в таком случае говорят, что имеет место равноускоренное вращение. Когда же угловая скорость остается постоянной, то угловое ускорение оказывается равным нулю и говорят о равномерном вращении тела.