Вопрос 2 § 43 физика 9 класс перышкин что служит источником электромагнитного поля?

Электрические поля и проводники

В статическом случае (т.е. когда заряды покоятся) электрическое поле внутри хорошего проводника отсутствует. Если бы в проводнике существовало электрическое поле, то на внутренние свободные электроны действовала бы сила, вследствие чего электроны пришли бы в движение
и двигались до тех пор, пока не заняли бы такое положение, при котором, напряженность электрического поля, а стало быть, и действующая на них сила обратились бы в нуль. Из этого рассуждения вытекают любопытные следствия. В частности, если проводник обладает результирующим зарядом, то этот заряд распределяется по внешней поверхности проводника. Этот факт можно объяснить с иной точки зрения. Если, например, проводник заряжен отрицательно, то мы легко можем представить, что отрицательные заряды отталкивают друг друга и устремляются
к поверхности проводника, чтобы расположиться как можно дальше друг от друга. Другое следствие состоит в следующем. Пусть положительный заряд Q помещен в центр полого изолированного проводника в форме сферической оболочки (рис. 22.22).
Поскольку внутри проводника электрического поля быть не может, силовые линии, идущие от положительного заряда, должны заканчиваться
на отрицательных зарядах на внутренней поверхности металлической сферы. В результате на внутренней поверхности сферического проводника будет индуцирован соответствующий отрицательный заряд -Q, а равный по величине положительный заряд +Q распределится по
внешней поверхности сферы (поскольку в целом оболочка нейтральна).
Таким образом, хотя внутри проводника электрическое поле отсутствует, снаружи сферы существует электрическое поле (рис. 22.22), как если бы металлической сферы вовсе не было.

С этим связано также и то обстоятельство, что силовые линии электрического поля всегда перпендикулярны поверхности проводника. Действительно, если бы вектор напряженности электрического поля Е имел компоненту, параллельную поверхности проводника, то электроны под действием силы двигались бы до тех пор, пока не заняли положение, в котором на них не действует сила, т. е. пока
вектор напряженности электрического поля не будет перпендикулярен поверхности.

Все сказанное относится только к проводникам. В изоляторах, у которых нет свободных электронов, может существовать электрическое поле и силовые линии не обязательно перпендикулярны поверхности.

Продолжение следует. Коротко о следующей публикации:
— Электрические диполи.
— Расчет напряженности электрического поля Е.
— Движение заряженной частицы в электрическом поле.

Альтернативные статьи: Электрический ток, Закон Ома.

Замечания и предложения принимаются и приветствуются!

История появления теории

Прежде чем физически было доказано существование этого явления, специалисты разных рангов пытались теоретически обосновать его появление. Первые попытки были осуществлены в конце XVIII века, когда астроном Лагранж ввел понятие потенциала.

Этот показатель характеризовал напряженность, а фактически является работой, которую должно совершить поле для перемещения заряда из бесконечности в определенную его точку. Чуть позже Кулон вывел понятие взаимодействия между заряженными частицами, для своих опытов он использовал крутильные весы.

В начале XIX века Пуассоном была доказана связь между понятием потенциала и электромагнитным явлением. Через 7 лет были проведены эксперименты, которые показали влияние на магнитную стрелку, протекающим по проводам током.

Это доказало, что вокруг проводников создается электрическое поле с неизменяемой напряженностью. Тему в дальнейшем продолжили Ом и Фарадей. Фарадей опубликовал работы, где описывал взаимодействие разнородных полей.

Негативное влияние электромагнитных полей

Электромагнитное поле может оказывать негативное влияние на окружающую среду и на здоровье человека.

Воздействие на природу

Фактор электромагнитного загрязнения окружающей среды служит одним из основных видов негативного техногенного воздействия на природу. ЭМ поле влияет на развитие растений и животных.

Влияние на животных и растения

Установлено, что электромагнитное загрязнение создает неблагоприятные условия для жизнедеятельности живых организмов. Так, вблизи ЛЭП замедляется рост растений, происходит изменение размеров и формы плодов, меняются цветки и стебли.

Электромагнитный фон, значительно превышающий нормальный природный уровень, негативно отражается на здоровье животных. В том числе установлено воздействие на нервную систему, что проявляется повышением агрессии, ухудшением сна и другими симптомами. У молодых животных замедляется рост. Также действие ЭМИ отражается на обмене веществ животных, на репродуктивной функции.

Механизм воздействия на организм человека

Электромагнитный смог постоянно окружает человека и оказывает мощное воздействие на здоровье. Механизм этого воздействия связан с разными факторами. Основным из них считается изменение свойств воды, которая является основой живой клетки. Это вызывает нарушения на клеточном уровне, которые могут иметь угрожающие здоровью последствия. Также зоне действие электротехнических приборов происходит нагрев тканей организма.

Результат длительного действия ЭМИ выражается в нарушениях со стороны большинства систем организма.

Влияние на нервную систему

Нервная система человека – самая уязвимая к электромагнитному излучению часть организма. В результате действия поля на клетки нарушается проницаемость ее мембраны для ионов кальция. Это приводит к тому, что в работе нервной системы возникают сбои со следующими клиническими проявлениями:

• изменения электроэнцефалограммы головного мозга;
• нарушения памяти;
• замедленная реакция;
• развитие депрессивных состояний.

Влияние на иммунную систему

Электромагнитное загрязнение является фактором, который негативно отражается на иммунной системе. Установлено, что регулярное воздействие ЭМИ вызывает общее ослабление иммунитета. Кроме того, может развиваться аутоиммунитет, что создает серьезную угрозу для здоровья.

Влияние на эндокринную систему

Воздействие ЭМИ на эндокринную систему приводит к повышению интенсивности выработки адреналина, и кортизола. Эти вещества относятся к гормонам стресса. Поэтому их выброс в организм может приводить к серьезным сбоям с такими проявлениями:

• повышение раздражительности и возбудимости;
• бессонница, нарушения сна;
• перепады артериального давления;
• слабость, головокружения и т.д.

Другие возможные реакции

Электросмог вызывает нарушения и во многих других системах организма

Примером может служить действие на сердечно-сосудистую систему, связанное с ухудшением проводимости миокарда, нарушениями сердечного ритма и другими сбоями, каким необходимо уделять серьезное внимание в связи с опасностью для жизни

Также демонстрирует уязвимость половая система. У женщин это проявляется сбоями в работе яичников. Воздействие электромагнитного загрязнения на мужчин к снижению подвижности сперматозоидов. Еще одним последствием становится проявление генетических нарушений у детей.

Способы защиты от электромагнитных волн

Полностью оградить себя и окружающую среду от электрических устройств и оборудования, создающего электромагнитное загрязнение, невозможно. Однако существуют меры по снижению вредного воздействия, которые можно применять в бытовой сфере:

• не устанавливайте электроприборы в одном месте, чтобы их магнитные поля не усиливали друг друга;
• избегайте ситуаций, когда рядом одновременно работают сразу несколько приборов, генерирующих мощное ЭМИ, например микроволновая печь, сотовый, телевизор, компьютер;
• включайте такие приборы только в заземленную розетку, не устанавливайте их в спальне, в зонах отдыха, рядом с обеденным и рабочим столом;
• старайтесь использовать электрические устройства меньшей потребляемой мощности;
• сократите время использования сотового телефона.

Энергия электрического поля

Виды энергии:
	Механическая	Потенциальная Кинетическая
‹›	Внутренняя
	Электромагнитная	Электрическая Магнитная
	Химическая
	Ядерная
G{\displaystyle G}	Гравитационная
∅{\displaystyle \emptyset }	Вакуума
Гипотетические:
	Тёмная
См.также:Закон сохранения энергии

Основная статья: Электромагнитная энергия

Электрическое поле обладает энергией. Плотность этой энергии определяется величиной поля и может быть найдена по формуле

u=12(E→D→),{\displaystyle u={\frac {1}{2}}\left({\vec {E}}{\vec {D}}\right),}

где E — напряжённость электрического поля, D — индукция электрического поля.

Сфера применения

Описываемое в данной статье явление обладает большой ролью в таких сферах, как медицина, химия, электротехника.

Использование в медицине

В медицине данное явление используется для улучшения кровообращения, восстановления поврежденных тканей, точечного прогревания, повышения температуры тела.

Медицинский УВЧ аппарат для прогревания

Применение в химии

В химии это явление применяется для разделения разнородных по составу жидкостей, фильтрации воды, удаления растворенных в веществах загрязнителей.

Электротехника

В электротехнике эта форма материи используется для беспроводной зарядки различных гаджетов (мобильных телефонов, планшетов) с помощью специального зарядного устройства, определения наличия в проводке напряжения бесконтактным способом (индикаторные отвертки на полевых транзисторах).

Граничные условия в электростатическом поле

Под
граничными условиями понимают условия,
которым удовлетворяет поле на границе
раздела двух различных сред. Прежде чем
перейти к обсуждению граничных условий,
рассмотрим поведение проводящего тела
в электростатическом поле. Проводящим
называется тело, в составе которого
имеются свободные заряды. Пусть некоторое
проводящее тело помещено в электростатическое
поле (рис.11.10). Тогда на каждый свободный
заряд со стороны поля начнет действовать
сила, под действием которой положительные
свободные заряды будут перемещаться в
сторону низкого потенциала, а отрицательные
– сторону высокого.
Перемещение зарядов
возможно только в пределах проводящего
тела, поэтому они скапливаются на его
поверхности (положительные – со стороны
низкого потенциала, а отрицательные –
со стороны высокого). Это
явление получило название электростатической
индукции, а скопившиеся на поверхности
проводника заряды называются
индуктированными.
Хотя сумма положительных
индуктированных зарядов в точности
равна сумме отрицательных и в целом
тело электрически нейтрально (если оно
не было предварительно заряжено), но
индуктированные заряды создают своё
поле, что приводит к изменению
результирующего поля внутри тела и
вблизи его и в его окрестности.

Все точки проводящего тела имеют
один и тот же потенциал, так как если
допустить, что между двумя точками
имеется разность потенциалов, то под
действием этой разности протечет ток
и потенциалы уравновесятся. Так как все
точки проводящего тела имеют один и тот
же потенциал, то напряженность
электростатического поля внутри его

т.е. поле внутри проводящего тела
отсутствует. С физической точки зрения
это объясняется тем, что внешнее поле
полностью компенсируется полем
индуктированных зарядов (см. рис.11.10).
Индуктированных зарядов наводится
именно столько и располагаются они
именно так, чтобы внутри проводящего
тела поля полностью компенсировались.
Таким образом, объём, занятый проводящим
телом является эквипотенциальным.
Описанное свойство проводящих тел
используется на практике для экранирования
аппаратуры от воздействия внешних
электростатических полей.

Условия на границе раздела
диэлектрика и проводящего тела.

На такой границе выполняются два условия:
для всех точек диэлектрика, непосредственно
примыкающих к поверхности проводника
равна нулю тангенциальная составляющая
напряженности поля (E
t
=0),
а вектор электрического смещения
численно равен поверхностной плотности
индуктированного заряда
(D=σ
).

Для
доказательства первого условия возьмём
две точки (1 и 2) на границе раздела
диэлектрик-проводник (рис.11.11).
Тангенциальная составляющая вектора
Е
будет
направлена по линии, соединяющей эти
точки и определится так
,
но
,
т.к. точки 1 и 2 принадлежат и проводнику,
а
поэтому
E
t
=0,
что и требовалось доказать.
Таким образом, силовые линии
электростатического поля подходят к
поверхности проводника под прямым углом
(E
t
=0).

Для
доказательства второго условия возьмем
произвольную точку на границе и окружим
её бесконечно малым плоским объёмом в
виде параллелепипеда (рис.11.12) и применим
к нему теорему Гаусса в интегральной
форме
.
Поскольку нижняя грань находится в
проводящей среде, то через неё поток
вектора D

равен нулю, также как и через боковые
грани (эти грани бесконечно малы, кроме
того вектор D

скользит вдоль них). Поток
вектора D

через верхнюю грань равен
,
т.к. векторы D

и
ds

совпадают по направлению.
Внутри поверхности
интегрирования находятся только
индуктированные заряды и их количество
равно
,
где

— поверхностная плотность индуктированного
заряда. Тогда

или
.

Условия
на границе раздела двух различных
диэлектриков.
На такой
границе выполняются два условия: для
всех точек, являющихся общими для двух
различных диэлектриков, равны по величине
тангенциальные составляющие вектора
Е
(Е
1 t =Е
2 t)и
нормальные
составляющие вектора D

(D
1n
=D
2n
).

Покажем справедливость первого
условия для чего возьмём произвольную
точку на границе раздела двух различных
диэлектриков и окружим её бесконечно
малым (длина
— dl
)
плоским (высота бесконечно
мала по сравнению с длиной) контуром
mnpq
(рис.11.13).
Составим
выражение циркуляции вектора
E

вдоль этого контура.
Сторона mn
находится
в верхней среде и, если контур обходить
по часовой стрелке, то составляющая
циркуляции вдоль этой стороны
.
Аналогично для стороны pq
D
Электростатическом
поле
направлено вертикально вверх…

Электрическое поле. ЗАДАЧИ с решениями

Формулы, используемые на уроках по теме «Электрическое поле. ЗАДАЧИ» в 10-11 классах при подготовке к ЕГЭ.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача № 1.
 Электрон движется без начальной скорости вдоль силовой линии однородного электрического поля напряженностью Е = 2 • 104 Н/Кл. Какой путь S он пролетит прежде, чем его скорость станет v = 100 км/с ? Среда — воздух. Модуль заряда электрона е = 1,6 • 10–19 Кл, его масса m_e = 9,1 • 10–31 кг.

Задача № 2.
 Пылинка с зарядом q = 1 нКл неподвижно висит в однородном электрическом поле напряженностью Е = 2 • 104 Н/Кл, вектор напряженности которого направлен вверх (рис. 2-9). Найти массу пылинки т. Сколько избыточных электронов N содержит пылинка? 

Задача № 3.
 Заряженный шар диаметром D находится в равновесии в жидком диэлектрике плотностью р₁ с диэлектрической проницаемостью ε (рис. 2-10). Найти поверхностную плотность зарядов на шаре σ, если плотность вещества шара р₂. Напряженность электрического поля в диэлектрике Е, вектор напряженности направлен вверх. 

Задача № 4.
На каком расстоянии г₂ от точечного заряда напряженность электрического поля этого заряда в жидком диэлектрике с диэлектрической проницаемостью ε₂ = 81 (вода) такая же, как на расстоянии r₁ = 9 см от этого заряда в воздухе?

Задача № 5.
 Электрон влетает в однородное электрическое поле со скоростью v, направленной перпендикулярно вектору напряженности Е (рис. 2-11). Под каким углом φ к линиям вектора напряженности будет направлен вектор его скорости через время t полета в поле? Чему будет равна работа сил поля А за это время? Чему будет равна кинетическая энергия электрона W_кчерез время t ? Напряженность поля Е. Масса электрона т_еи его заряд е известны. 

Задача № 6.
 Тонкая металлическая пластинка массой m падает вертикально вниз равноускоренно так, что ее плоскость остается горизонтальной. Падению пластинки противодействует сила сопротивления среды F_соnp. Найти напряженность электрического поля Е, возникающего внутри пластинки вследствие инерции свободных электронов. Масса электрона m_e, его заряд е.

Задача № 7.
 К бесконечной, вертикальной, равномерно заряженной плоскости прикреплена одним кондом невесомая нить, на другом конце которой находится одноименно с нитью заряженный шарик радиусом R = 0,5 см, несущий заряд q = 1 • 10–10 Кл. Плотность вещества шарика р = 2 • 103 кг/м3. Натяжение нити F_н = 4,9 • 10–2 Н. Какой угол а образует с плоскостью нить, на которой висит шарик (рис. 2-12)? Среда – воздух. Чему равна поверхностная плотность σ зарядов на плоскости? 

Задача № 8.
 Сфера радиусом R = 1 см равномерно заряжена. Поверхностная плотность зарядов на сфере σ = 10 нКл/см2. Найти напряженность Е₁ электрического поля на расстоянии r₁ = 10 см от центра сферы (рис. 2-13). Построить график зависимости напряженности Е от расстояния r в пределах от r = 0 до r₁ = 10 см. Среда — воздух. 

Задача № 9.
 Заряды q₁ = 20 нКл и q₂ = 10 нКл расположены на расстоянии r = 10 см друг от друга. Найти напряженность электрического поля Е₁, созданного этими зарядами в точке 1, расположенной на расстоянии r₁ = 4 см от заряда q₁ и напряженность Е₂ в точке 2, расположенной на расстоянии г₂ = 2 см от заряда q₂ (рис. 2-15). Среда — вакуум.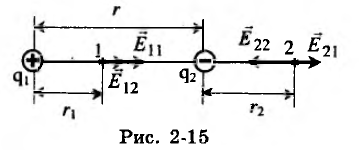 

Задача № 10.
 Два одноименных точечных заряда q и 4q расположены на расстоянии r друг от друга. На каком расстоянии r₁ от заряда q находится точка М, в которой напряженность поля этих зарядов Е = 0? На каком расстоянии r₂ от заряда q находится такая точка, если эти заряды разноименные?

Задача № 11.
 На расстоянии г = 3 см от поверхности шара радиусом R = 2 см находится точечный отрицательный заряд q = –2 нКл. Шар заряжен положительно с поверхностной плотностью зарядов σ = 2 нКл/м2. Найти напряженность поля Е, созданного заряженным шаром и точечным зарядом, в точке, расположенной на расстоянии r₁ = 4 см от центра шара, и г₂ = 3 см от заряда q. Среда — воздух.

Задача № 12.
 В вершинах равностороннего треугольника со стороной а находятся заряды q, –q и q. Найти напряженность поля Е, созданного этими зарядами в центре треугольника. Среда — воздух.

(с) В учебных целях использованы цитаты из учебного пособия «Новый репетитор по физике для подготовки к ЕГЭ : задачи и методы их решения / И.Л. Касаткина; под ред. Т.В. Шкиль. — Ростов н /Д : Феникс».

Это конспект по теме «Электрическое поле. ЗАДАЧИ с решениями». Выберите дальнейшие действия:

• Вернуться к списку конспектов по Физике.
• Проверить свои знания по Физике.

Описание физического явления

Обнаружить наличие электрического поля несложно. Для этого нужно обладать заряженной частицей и поместить ее в определенное место в пространстве.

Если на нее начнет воздействовать электрическая сила, это и будет доказательством его наличия.

Свойствами поля являются:

• невидимость;
• способность взаимодействовать только с другими электрическими полями;
• оно обладает векторным направлением;
• поле может притягивать или отталкивать;
• возникает всегда вокруг заряженных частиц;
• концентрация;
• неоднородность.

На заряженную частицу, помещенную в поле, с разных точек действуют силы, которые отличаются значением и направлением. Для ее определения существует силовая характеристика поля, которая называется напряженностью и обозначается латинской Е.

История развития электрического поля

Основными вехами истории развития учения о данном явлении являются следующие открытия:

• 1773 г. – французский астроном Ж.Л. Лангранж впервые применяет такое понятие, как «потенциал». Примененное относительно небесных тел это понятие в дальнейшем стало широко использоваться в физике.
• 1785 – Шарль Кулон сформулировал названный позднее его именем закон, описывающий взаимодействие заряженных частиц;
• 1812 – французский физик С.М. Пуассон применил понятие «потенциал» в описании электрических, электромагнитных процессов и явлений;
• 1819 – датский физик Х.К. Эрстед опытным путем показал влияние протекающего по проводнику тока на отклонение магнитной стрелки, происходящее под воздействием образующегося вокруг него электрополя;
• 1827 – Г. Омом сформулирован названный его именем основной закон электротехники, описывающий соотношение основных характеристик протекающего по проводнику электрического тока (напряжения, силы, сопротивления);
• 1831 – М. Фарадей, ученик известного британского ученого Гемфри Дэви, в своем труде по электромагнетизму описывает взаимодействие двух составляющих электромагнитного поля;
• 1873 –Д.К. Максвелл издает свой знаменитый фундаментальный труд «Трактат об электричестве и магнетизме», в котором ученый подробно описывает взаимодействие электрического и магнитного полей, приводит уравнения, описывающие их закономерность.

Д.К. Максвелл

Виды и характеристики волн

Окружающий нас электромагнитный фон создается различными видами излучений. В том числе выделяют такие основные виды ЭМ волн:

• Радиоволны – электромагнитные поля, создаваемые при работе оборудования и бытовых приборов, а также в результате атмосферных явлений. В зависимости от длины волны бывают ультракороткими, короткими, средними, длинными и сверхдлинными.
• Инфракрасное излучение. Световое излучение с длиной волны от 1 мм до 780 нм и частотой до 429 ТГц.
• Световое излучение видимого спектра. Длина волны составляет 400-780 нм при частоте в пределах 790-385 ТГц.
• Ультрафиолетовое излучение. Длина волны меньше 400 нм, может доходить до 10 нм. Частота – до 3х1016 Гц.
• Рентгеновское излучение. Длина в диапазоне от 10 нм до 5пм. Частота – до 3х1019 Гц.
• Гамма излучение. Все электромагнитные волны с длиной волны меньше, а частотой – больше рентгеновского излучения.

Силовые линии

Коль скоро электрическое поле является векторным, его можно изображать в различных точках стрелками, как это сделано на рис. 22.13. Направления векторов Еа, Еb, Ес совпадали бы с направлениями показанных на этом рисунке сил и лишь длина их была бы уже иной в результате деления на q. Отношение длин векторов Еа, Еb, Ес сохранится прежним, так как мы делим на один и тот же заряд. Однако изображать электрическое поле таким образом неудобно, поскольку при большом числе точек весь рисунок будет испещрен стрелками. Поэтому пользуются другим способом изображения поля-методом силовых линий.

Для наглядного представления электрического поля его изображают семейством линий, указывающих направление напряженности поля в каждой точке пространства.
Эти так называемые силовые линии проводятся так, чтобы указывать направление силы, действующей в данном поле на положительный пробный заряд. Силовые линии точечного положительного заряда показаны на рис. 22.20, а, отрицательного — на рис. 22.20,6.
В первом случае линии радиально расходятся от заряда, во втором они радиально сходятся к заряду. Именно в таком направлении будут
действовать силы на положительный пробный заряд. Конечно, силовые линии можно нанести и в промежутках между изображенными на рисунке

Но мы условимся наносить силовые линии с таким расчетом, чтобы число линий, исходящих от положительного заряда или заканчивающихся на отрицательном заряде, было пропорционально величине этого заряда.
Обратим внимание на то, что вблизи заряда, где сила максимальна, линии расположены более тесно. Это общее свойство силовых линий: чем теснее расположены силовые линии, тем сильнее электрическое поле в этой области

Вообще говоря, можно всегда изображать силовые линии таким образом, чтобы число линий, пересекающих единичную площадку,
перпендикулярную направлению поля Е, было пропорционально напряженности электрического поля. Например, для уединенного точечного заряда (рис. 22.20) напряженность электрического поля убывает как 1/r 2; так же будет уменьшаться с расстоянием и число равномерно распределенных силовых линий, пересекающих единичную площадку: ведь общее число силовых линий остается
постоянным, а площадь поверхности, через которую они проходят, растет как 4πr 2 (поверхность сферы радиусом
г). Соответственно число силовых линий на единицу площади пропорционально 1/r 2.

На рис. 22.21, а показаны силовые линии поля, создаваемого двумя зарядами противоположных знаков. Здесь силовые линии искривлены и направлены от положительного заряда к отрицательному. Поле в любой точке направлено по касательной к силовой линии, как показано
стрелкой в точке Р.
На рис. 22.21,6 и в показаны силовые линии электрического поля двух положительных зарядов и поля между двумя параллельными
противоположно заряженными пластинами. Заметим, что силовые линии поля между пластинами параллельны и расположены на равном расстоянии друг от друга, исключая область вблизи краев.

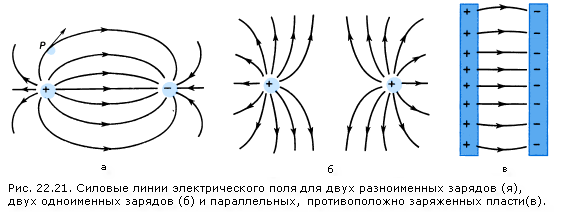
Таким образом, в центральной области напряженность электрического поля во всех точках одинакова, и мы можем написать:Е = const (между близко расположенными параллельными пластинами).
Хотя вблизи краев это не так (силовые линии изгибаются), часто этим можно пренебречь, особенно если расстояние между пластинами мало по сравнению с их размерами. .

Итак, силовые линии обладают следующими свойствами:

1. Силовые линии указывают направление напряженности электрического поля: в любой точке напряженность поля направлена по касательной к силовой линии.

2. Силовые линии проводятся так, чтобы напряженность электрического поля Е была пропорциональна числу линий, проходящих через единичную площадку, перпендикулярную линиям.

3. Силовые линии начинаются только на положительных зарядах и заканчиваются только на отрицательных зарядах; число линий, выходящих из заряда или входящих в него, пропорционально величине заряда.

Можно также сказать, что силовая линия электрического поля — это траектория, по которой следовал бы помещенный в поле малый пробный заряд. (Строго говоря, это верно лишь в том случае, если пробный заряд не обладает инерцией или движется медленно, например вследствие
трения.)
Силовые линии никогда не пересекаются. (Если бы они пересекались, это означало бы, что в одной и той же точке напряженность электрического поля имеет два различных направления, что лишено смысла.)

Примечания

1. М. А. Миллер, Г. В. Пермитин. // Физическая энциклопедия : / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия (тт. 1—2); Большая Российская энциклопедия (тт. 3—5), 1988—1999. — ISBN 5-85270-034-7.
2. Электрическое поле // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
3. Гринберг Г. А. Избранные вопросы математической теории электрических и магнитных явлений. — М.: АН СССР, 1948. — 727 с.
4. Миролюбов Н. Н., Костенко М. В., Левинштейн М. Л. Методы расчета электростатических полей. — М.: Высшая школа, 1963. — 416 с.
5. Смайт В. Электростатика и электродинамика. — М.: ИЛ, 1954. — 604 с.
6. ↑ Колечицкий Е. С. Расчет электрических полей устройств высокого напряжения. — М.: Энергоатомиздат, 1983. — 168 с.

Графическая картина электростатического поля

Электростатическое
поле определено, если
известен закон изменения
напряженности и потенциала в функции
координат. Нагляднее же его можно
охарактеризовать совокупностью силовых
и эквипотенциальных линий, которая и
называется его графической картиной.
Силовой называется такая мысленно
проведенная в поле линия, которая
начинается на положительно заряженном
теле, заканчивается на отрицательно
заряженном теле и касательная к которой
в любой точке дает направление вектора
Е
. Вдоль силовой
линии перемещался бы весьма малый
положительный заряд, имеющий возможность
свободно двигаться и не обладающий
инерцией. Так как положительный и
отрицательный заряды не могут находиться
в одной точке, то силовые линии имеют
начало и конец, они не могут быть
замкнутыми сами на себя. В любом
электростатическом поле могут быть
проведены эквипотенциальные поверхности
как совокупности точек, имеющих один и
тот же потенциал. Если поле рассечь
какой либо плоскостью, то в полученном
сечении будут видны следы эквипотенциальных
поверхностей, которые и называются
эквипотенциальными линиями. В
противоположность силовым эквипотенциальные
линии являются непрерывными, замкнутыми
сами на себя. В любой точке поля силовые
и эквипотенциальные линии перпендикулярны
друг другу. Для примера приведем
графическую картину электростатического
поля двух точечных зарядов (рис.11.2).

C
вязь
между напряженностью поля и потенциалом

Выясненная ранее взаимосвязь
напряженности и потенциала

называется интегральной. На практике
же чаще используется дифференциальная
связь между этими величинами для
выяснения которой выделим в некотором
электростатическом поле две
эквипотенциальные линии (рис.11.3). Пусть
все точки первой линии обладают
потенциалом φ
1 ,
а второй – φ
2 .
Для определенности будем полагать, что
φ
1 >φ
2 ,
но отличаются они на бесконечно малую
величину, т.е. φ
1 —φ
2 =d
φ
.
Расстояние между линиями – dl
.
Выберем на первой линии
произвольную точку 1, а на второй – точку
2. Если разность потенциалов между этими
точками поделить на кратчайшее расстояние
между ними (по прямой), то полученная
величина будет характеризовать скорость
изменения потенциала в направлении
кратчайшего расстояния между точками.
Эта скорость зависит от того, как выбраны
точки. Если, например, точку 2 смещать
вверх, то она упадет, поскольку не d
φ

изменится, а расстояние между точками
возрастет. Если т.2 смещать вниз, то
происходит возрастание указанной
скорости. Когда т.2 займет положение,
наиболее близкое к т.1 (т.3), скорость
изменения потенциала станет максимальной.
В математике вводится понятие градиента
скалярной функции, как скорости её
изменения, взятой в направлении
наибольшего возрастания. Применим это
понятие к потенциалу, т.е. рассмотрим
grad
φ
.
Это будет вектор – он
имеет направление от т.3 к т.1 (направление
наибольшего возрастания), а его модуль
равен

Напряженность поля направлена от более высокого
потенциала (φ
1)
к меньшему (φ
2),
а её модуль равен

(см. интегральную форму). Поскольку
модули векторов Е

и gradφ
одинаковы,
а направлены они в противоположные
стороны, то
.

Направление
наибольшего возрастания потенциала в
общем случае не совпадает ни с какой
координатной осью, поэтому grad
φ
представляется в виде
суммы проекций по координатным осям,
например, в прямоугольной системе
координат (рис.11.4)

где

— орты (единичные векторы) прямоугольной
системы,

— скорости изменения потенциала вдоль
соответствующей оси. Напряженность Е

также может быть записана через проекции

Два вектора равны друг другу, если у них
одинаковы проекции, т.е.

Именно последние три формулы используются
в практических расчетах.

Для сокращения записи различных
операций в теории поля широко используется
не имеющий физического смысла
дифференциальный оператор Гамильтона
(набла), под которым понимают сумму
частных производных по координатным
осям, умноженных на соответствующие
орты. В декартовой системе координат
он имеет вид:

Формально набла можно рассматривать
как вектор. Он может быть применен как
к скалярной, так и к векторной функции.
Та функция, действие над которой
производят (дифференцирование по
координатным осям или пространственное
дифференцирование) пишется справа от

Если справа отне
указана функция, то сам по себе оператор
набла не применяется (аналогично как
sin, log
и т.д.). Применив оператор набла к
потенциалу

и сравнив его с
,
видим, что
=
(для скалярной функции частная и полная
производные совпадают). Тогда связь
между напряженностью и потенциалом
может быть записана так: