Гидродинамика. основополагающие термины гидродинамики

Виды течения жидкостей и газов

Ламинарное течение — течение, при котором жидкость или газ перемещается слоями без перемешивания и пульсаций (то есть беспорядочных быстрых изменений скорости и давления).

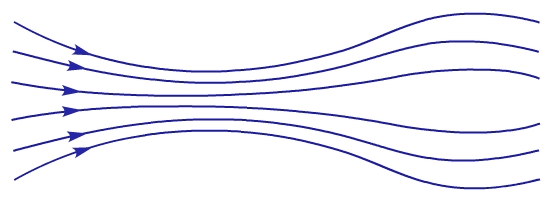
Турбулентное течение — течение жидкости или газа, характеризующееся беспорядочным, нерегулярным перемещением его объёмов и их интенсивным перемешиванием, но в целом имеющее плавный, регулярный характер.

Стационарное течение — течение, в каждой точке которого, скорость жидкости не меняется во времени. Ламинарное течение может быть стационарным, турбулентное — не может.

Существует жидкое трение. При движении тела в жидкости или газе возникают силы сопротивления в виде силы жидкого трения.

История гидродинамики

Первые попытки исследования сопротивления среды движению тела были сделаны Леонардо  да Винчи и Галилео Галилеем. Принято считать, что Галилео проводил опыты по сбрасыванию шаров различной плотности с Пизанской башни, данный опыт описывается в учебной литературе и поэтому известен всем со школьных времён (достоверной информации, подтверждающей проведение данного опыта Галилео Галилеем на сегодняшний день не имеется). В 1628 году Бенедетто Кастелли издал маленькую работу, в которой он очень хорошо для своего времени объяснил несколько явлений при движении жидкости в реках и каналах. Однако, в работе содержалась ошибка, так как он предполагал скорость вытекания жидкости из сосуда пропорциональной расстоянию отверстия до поверхности воды. Торричелли заметил, что вода, выливающаяся из фонтана поднимается на высоту порядка уровня воды питающего водоёма. На основе этого он доказал[источник не указан 1828 дней] теорему, о пропорциональности скорости вытекания квадратному корню из расстояния от отверстия до поверхности жидкости. Теорема была экспериментально проверена на воде, вытекающей из различных насадок. Едме Мариотто в труде, который был опубликован после его смерти впервые объяснял несоответствие теории и экспериментов при помощи учёта эффектов трения. В труде Исаака Ньютона «philosophie naturalis principia mathematica» для объяснения снижения скорости проточной воды использовались именно понятия вязкости и трения. Также в работах Ньютона развивались представления Мариотто о потоке воды как о наборе трущихся нитей. Эта теория уже сопоставима с современной теорией переноса движения в жидкостях.

После издания Ньютоном своих работ учёные всего мира начали пользоваться его законами для объяснения различных физических явлений. Спустя 60 лет Леонард Эйлер получил аналог второго закона Ньютона для жидкости. В 1738 году Даниил Бернулли издал работу, где объяснялась теория движения жидкостей. Он использовал два предположения: поверхности жидкости, вытекающей из сосуда всегда остаётся горизонтальной[источник не указан 1828 дней] и то, что скорость опускания слоев воды обратно пропорциональна их ширине. В отсутствии демонстраций этих принципов теория доверия не получила.

Колин Маклорен и Иоанн Бернулли хотели создать более общую теорию, зависящую только от фундаментальных законов Ньютона. Научное сообщество сочло их методы недостаточно строгими. Теория Даниила Бернулли встретила сопротивление со стороны Жана Лерона Даламбера, разработавшего свою теорию. Он применил принцип, полученный Якобом Бернулли, который сводил законы движения тел к закону их равновесия. Даламбер применил этот принцип для того, чтобы описать движение жидкостей. Он использовал те же гипотезы, что и Даниил Бернулли, хотя его исчисление было выстроено в другой манере. Он рассматривал в каждый момент движения слоя жидкости составленным из движения в прошлый момент времени и движения, который он потерял. Законы равновесия между потерями и потерями движения дали уравнения, представляющее уравнение движение жидкости. Оставалось выразить уравнениями движение частицы жидкости в любом заданном направлении. Эти уравнения были найдены Даламбером из двух принципов: прямоугольный канал, выделенный в массе жидкости, находящейся в равновесии, сам находится в равновесии и часть жидкости, переходящая из одного места в другое сохраняет тот же самый объём, если она является несжимаемой и изменяет объём с учётом законов упругости, в противном случае. Этот метод был перенят и доведён до совершенства Леонардом Эйлером. Решение вопроса о движении жидкостей было произведено с помощью метода частных производных Эйлера. Это исчисление было впервые применено к движению воды Даламбером. Метод позволил представить теорию движения жидкостей в формулировке, не ограниченной никакими особыми предположениями.

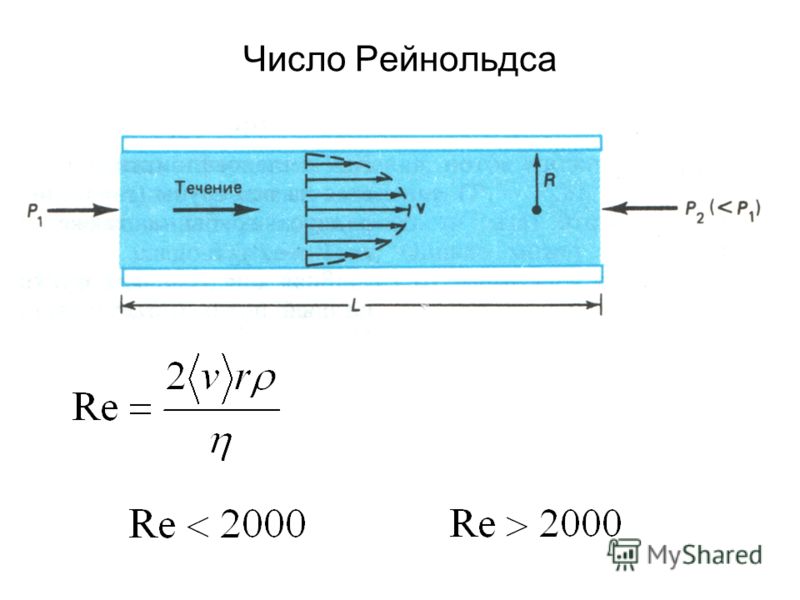
Критерий Рейнольдса

Такую зависимость вывел английский физик и инженер Осборн Рейнольдс (1842 — 1912).

Критерий, который помогает ответить на вопрос, есть ли необходимость учитывать вязкость, является число Рейнольдса Re. Оно равно отношению энергии движения элемента текущей жидкости к работе сил внутреннего трения.

Рассмотрим кубический элемент жидкости с длиной ребра n. Кинетическая энергия элемента равна:

Согласно закону Ньютона, сила трения, действующая на элемент жидкости, определяется так:

Работа этой силы при перемещении элемента жидкости на расстояние n составляет

а отношение кинетической энергии элемента жидкости к работе силы трения равно

Сокращаем и получаем:

Re — называется числом Рейнольдса.

Таким образом, Re — это безразмерная величина, которая характеризует относительную роль сил вязкости.

Например, если размеры тела, с которым соприкасаются жидкость или газ, очень малы, то даже при небольшой вязкости Re будет незначительно и силы трения играют преобладающую роль. Наоборот, если размеры тела и скорость велики, то Re >> 1 и даже большая вязкость почти не будет влиять на характер движения.

Однако не всегда большие числа Рейнольдса означают, что вязкость не играет никакой роли. Так, при достижении очень большого (несколько десятков или сотен тысяч) значения числа Re плавное ламинарное (от латинского lamina — «пластинка») течение превращается в турбулентное (от латинского turbulentus — «бурный», «беспорядочный»), сопровождающееся хаотическими, нестационарными движениями жидкости. Этот эффект можно наблюдать, если постепенно открывать водопроводный кран: тонкая струйка течёт обычно плавно, но с увеличением скорости воды плавность течения нарушается. В струе, вытекающей под большим напором, частицы жидкости перемещаются беспорядочно, колеблясь, всё движение сопровождается сильным перемешиванием.

Появление турбулентности весьма существенно увеличивает лобовое сопротивление. В трубопроводе скорость турбулентного потока меньше скорости ламинарного потока при одинаковых перепадах давления. Но не всегда турбулентность плоха. В силу того что перемешивание при турбулентности очень значительно, теплообмен — охлаждение или нагревание агрегатов — происходит существенно интенсивнее; быстрее идёт распространение химических реакций.

Поток жидкости. Объемный расход.

Линия тока — траектория по которой движется данная частица жидкости. Скорость движения тока по отношению к траектории направлена по касательной. Линии тока не могут пересекаться, потому что в данной точке пространства скорость направлена только в одном направлении.

Трубка тока — пучок линий тока ограниченный замкнутым контуром. За пределы трубки тока жидкость вытечь не может. Например — водопроводная труба или Гольфстрим.

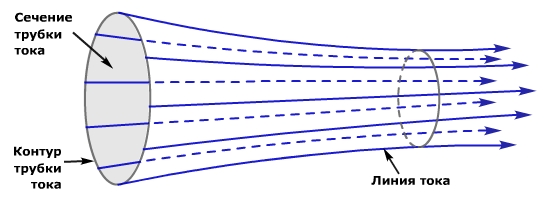
Поток жидкости через данное сечение (объемный расход) (Q) — физическая величина, равная отношению объема жидкости (V) протекающей через это сечение за некоторый промежуток времени (t) к длительности этого промежутка (Q = V/t).

Давайте выясним от чего зависит поток. Рассмотрим простую ситуацию. У нас есть труба с сечением площадью S. В ней движется поток со скоростью v. За время t жидкость проходит по трубе расстояние l или v*t. Объем расхода будет равный v*t*S. Подставляя значение в формулу получим Q = S*v.

Объемный расход трубы

S — площадь сечения трубы;v — скорость потока;R — радиус трубы;

Жидкость в трубе переменного сечения

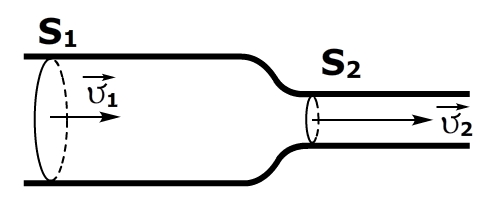
Что можно сказать об объемах жидкости прошедших через одно и тоже время через сечение S₁ и через сечение S₂? Они одинаковы, потому что жидкость несжимаема. Значит от сюда следует, что Q₁ = Q₂. От сюда следует S₁*v₁=S₂*v₂. Или для любого сечения с перпендикулярной скоростью потока S*v=const.

Понятие гидродинамики

Гидродинамика — раздел гидравлики, в котором рассматриваются законы движения и взаимодействия жидкости с неподвижными и подвижными поверхностями.

Движение жидкости существенно отличается от движения твердого тела. При движении жидкости расстояние между ее частицами не остается постоянным. Перемещение достаточно малого объема жидкости можно представить в виде суммы трех движений — поступательного, вращательного движения всего объема в целом, а также перемещения различных частиц объема относительно друг друга. В движущейся жидкости учитывают как массовые силы, так и силы трения (вязкость).

Движущаяся жидкость характеризуется двумя параметрами: скоростью течения v и гидродинамическим давлением р. Основной задачей гидродинамики является определение этих параметров при заданной системе внешних сил.

При движении жидкости скорость и давление могут изменяться в пространстве и во времени. В связи с этим различают два вида движения жидкости: установившееся и неустановившееся.

Установившимся называется движение, при котором скорость и давление в каждой точке пространства, занятого жидкостью, не изменяются во времени и является функцией только ее координат, т. е.

При неустановившемся движении давление р и скорость v изменяются в каждой точке не только с изменением координат, но и во времени:

Под жидкой частицей в гидродинамике понимают условно выделенный очень малый объем жидкости, изменением формы которого можно пренебречь. Каждая частица жидкости при движении описывает кривую, которая называется траекторией движения.

Под потоком жидкости понимают движущуюся массу жидкости, полностью или частично ограниченную поверхностями. Поверхности раздела могут быть твердыми или образованными самой жидкостью на границе раздела фаз. Границами потоков служат стенки труб, каналов, открытая поверхность жидкости, а также поверхность обтекаемых потоком тел.

Напорным называется движение потока в закрытых руслах при полном заполнении поперечного сечения жидкостью. Например, напорное движение в трубах. Оно возникает за счет разности давлений в начале и конце трубопровода.

Безнапорным называется движение жидкости в открытых руслах, когда поток имеет свободную поверхность. В этом случае движение осуществляется только за счет сил тяжести, т. е. при наличии уклона (движение воды в каналах, реках, лотках и т. д.).

Струи представляют собой потоки жидкости, вытекающие через отверстия или сопла под действием напора. Струи могут быть ограничены со всех сторон газообразной или жидкой средой. В первом случае они называются свободными, во втором — затопленными.

Линией тока называют воображаемую кривую в движущемся потоке жидкости, для которой векторы скоростей каждой из частиц жидкости, находящихся на ней в данный момент времени, являются касательными к этой кривой (рис.1).

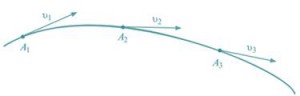
Рис. 1. Линия тока

Линия тока при установившемся движении совпадает с траекторией частиц. Для неустановившегося движения линии тока не совпадают с траекторией. Линия тока характеризует направление движения всех частиц, расположенных на ней в данный момент, а траектория представляет собой путь, пройденный одной частицей за какое-то время τ.

Литература

• Иванов Б. Н. Мир физической гидродинамики: От проблем турбулентности до физики космоса. Изд.2,— М.: URSS, 2010.— 240 с.
• Falkovich, G (2011), , Cambridge Univ Press, ISBN 978-1-107-00575-4, http://www.cambridge.org/us/academic/subjects/physics/nonlinear-science-and-fluid-dynamics/fluid-mechanics-short-course-physicists> * Фалькович Г. (2014), , РХД, http://www.weizmann.ac.il/complex/falkovich/fluid-mechanics>
• Truesdell, Clifford Ambrose. Rational fluid mechanics, 1687–1765. Editor’s introduction to Euleri Opera omnia II 12 // Leonardi Euleri. Opera Omnia. — Lausanne: Auctoritate et Impensis, Societas Scientiarum Naturalium Helveticae, 1954. — Т. 12. — С. I—CXXV. — (II).

Два способа описания движения жидкости или газа

Первый подход к описанию движения

Берут какую-то частицу жидкости или газа, точнее очень малый объем, настолько не большой, что его размерами можно пренебречь относительно той области в которой он движется. И рассматривают силы, действующие на эту частицу. Что это за силы? Это сила тяжести и сила давления. Зная силы действующие на частицу, с помощью 2-го закона Ньютона мы можем найти ускорение этой частицы. Зная ускорение, пользуясь аппаратом кинематики чисто математическим путем мы можем вычислить как меняется её скорость и направление. Зная как меняется скорость мы можем найти перемещение частицы в любой момент времени, т.е. мы можем знать траекторию движения частицы. Это невообразимо сложная задача, потому что таких частиц очень много, они движутся одновременно. Поэтому такой подход используется с помощью компьютерного моделирования. Именно такую задачу для огромного количества частиц решают суперкомпьютеры.

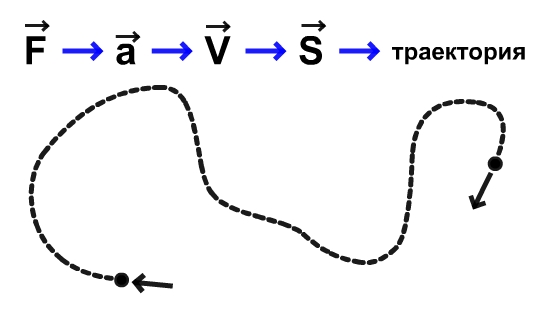
Второй подход к описанию движения

Этот подход более уместен, когда мы анализируем на теоретическом уровне движение жидкостей. Идея состоит в следующем. При первом подходе мы рассматриваем каждую частицу отдельно. При втором подходе мы рассматриваем жидкость как совокупность частиц. И в один момент времени смотрим как движутся частицы во всех точках жидкости сразу и рассматриваем систему как векторное поле скоростей.

Уравнение Бернулли стационарного движения

Одно из важнейших уравнений гидромеханики было получено в 1738 г. швейцарским учёным Даниилом Бернулли (1700 — 1782). Ему впервые удалось описать движение идеальной жидкости, выраженной в формуле Бернулли.

Идеальная жидкость — жидкость, в которой отсутствуют силы трения между элементами идеальной жидкости, а также между идеальной жидкостью и стенками сосуда.

Уравнение стационарного движения, носящее его имя, имеет вид:

где P — давление жидкости, ρ − её плотность, v — скорость движения, g — ускорение свободного падения, h — высота, на которой находится элемент жидкости.

Смысл уравнения Бернулли в том, что внутри системы заполненной жидкостью (участка трубопровода) общая энергия каждой точками всегда неизменна.

В уравнении Бернулли есть три слагаемых:

• ρ⋅v2/2 — динамическое давление — кинетическая энергия единицы объёма движущей жидкости;
• ρ⋅g⋅h — весовое давление — потенциальная энергия единицы объёма жидкости;
• P — статическое давление, по своему происхождению является работой сил давления и не представляет собой запаса какого-либо специального вида энергии («энергии давления»).

Это уравнение объясняет почему в узких участках трубы растёт скорость потока и падает давление на стенки трубы. Максимальное давление в трубах устанавливается именно в месте, где труба имеет наибольшее сечение. Узкие части трубы в этом отношении безопасны, но в них давление может упасть настолько, что жидкость закипит, что может привести к кавитации и разрушению материала трубы.

Движение жидкости

Движение жидкости зависит от многих факторов, учесть которые очень трудно. Поэтому действительное движение заменяют упрошенной моделью. В основе гидродинамики лежит струйчатая модель движения, которая предполагает, что поток жидкости состоит из бесконечно большого числа элементарных струек.

Если в потоке движущейся жидкости выделить элементарную площадку δF ограниченную контуром К, и через все его точки провести линии тока, то образуется трубчатая поверхность, называемая трубкой тока (рис. 2). Жидкость, движущаяся внутри трубки тока, называется элементарной струйкой (см. рис. 2).

Сечение, расположенное нормально к линиям тока, называется живым сечением элементарной струйки.

Элементарная струйка при установившемся движении обладает следующими свойствами:

• ее форма и ориентация в пространстве остаются неизменными во времени;
• боковая поверхность струйки непроницаема для жидкости, т.е. ни одна частичка жидкости не может проникнуть внутрь или выйти наружу через боковые стенки трубки тока;
• ввиду малости живого сечения струйки скорость и давление во всех точках этого сечения следует считать одинаковыми. Однако вдоль струек значения скорости v и давления р в общем случае могут изменяться.

Рис. 2.. Трубка тока: К — контур жидкости

Живым сечением потока F называется площадь сечения потока, перпендикулярная к направлению линий тока и ограниченная его внешним контуром. Площадь живого сечения потока (рис. 3.) равна сумме площадей живых сечений элементарных струек.

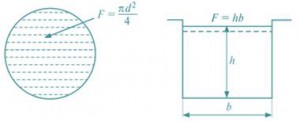
Рис. 3. Площадь живого сечения потока

Смоченным периметром потока П называется длина контура живого сечения, по которой жидкость соприкасается с ограничивающими ее стенками. При напорном движении жидкости смоченный периметр П совпадает с геометрическим периметром П_г, при безнапорном не совпадает (рис. 4).

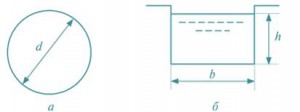
Рис. 4. Смоченный периметр:

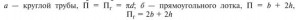
Гидравлическим радиусом R_г называется отношение площади живого сечения к смоченному периметру:

Геометрический радиус и гидравлический радиус — совершенно разные понятия, даже в случае напорного движения жидкости в круглой трубе.

Например, для трубы диаметром d  геометрический радиус

r=d/2, а гидравлический 

При гидравлических расчетах часто используется понятие эквивалентного диаметра:

Для круглых напорных труб диаметром d

Для труб прямоугольного сечения

Расходом называется количество жидкости, протекающей через живое сечение потока в единицу времени. Различают объемный V_c, массовый М_си весовой G_c расходы жидкости. Между ними существует связь:

Для элементарной струйки элементарный расход определяется по формуле:

где dF — площадь живого сечения элементарной струйки.

Объемный расход потока равен сумме элементарных расходов струек.

Скорость жидкости в различных точках живого сечения потока различна, и точный закон изменения скорости по сечению не всегда известен, поэтому для упрощения расчетов вводят понятие средней скорости для данного живого сечения ν_cp, тогда:

Средняя скорость — фиктивная скорость потока, которая считается одинаковой для всех частиц данного сечения и подобрана так, что расход, определенный по ее значению, равен истинному значению расхода (рис. 5).

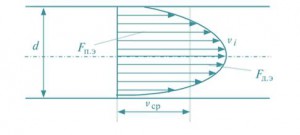
Рис. 5. К понятию «средняя скорость»:

F п.э. — площадь прямоугольной эпюры скоростей (средних);

F_д.э. — площадь действительной (криволинейной) эпюры

Установившееся движение характеризуется постоянством расхода во времени. Различают равномерное и неравномерное установившееся движение.

Равномерным установившимся движением называется такое движение жидкости, при котором средняя скорость и площади живых сечений потока не изменяются по его длине, например установившееся движение в цилиндрической трубе, движение в канале призматической формы (рис. 6).

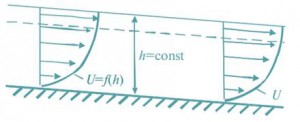
Рис. 6. Равномерное движение в канале призматической формы

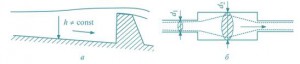
Рис. 7. Примеры возникновения неравномерного движения: а — перед подпорным сооружением; б — при внезапном сужении

Неравномерным установившемся движением называется такое движение, при котором средняя скорость и площади живых сечений изменяются по длине, например движение в трубе переменного сечения, движение в открытых руслах при наличии перегораживающих сооружений (рис. 7).

Гидравлика

Уравнение Навье — Стокса для вязких жидкостей

В более строгой формулировке линейная зависимость вязкого трения от изменения скорости движения жидкости называется уравнением Навье — Стокса. Оно учитывает сжимаемость жидкостей и газов и, в отличие от закона Ньютона, справедливо не только вблизи поверхности твёрдого тела, но и в каждой точке жидкости (у поверхности твёрдого тела в случае несжимаемой жидкости уравнение Навье — Стокса и закон Ньютона совпадают).

Любые газы, для которых выполняется условие сплошной среды, подчиняются и уравнению Навье — Стокса, т.е. являются ньютоновскими жидкостями.

Вязкость жидкости и газа обычно существенна при относительно малых скоростях, потому иногда говорят, что гидродинамика Эйлера — это частный (предельный) случай больших скоростей гидродинамики Навье — Стокса.

При малых скоростях в соответствии с законом вязкого трения Ньютона сила сопротивления тела пропорциональна скорости. При больших скоростях, когда вязкость перестаёт играть существенную роль, сопротивление тела пропорционально квадрату скорости (что впервые обнаружил и обосновал Ньютон).