Гидравлический расчет трубопровода

Приложение

Вывод уравнения Бернулли

Энергия маленького элемента жидкости: E=mv22+U{\displaystyle E={\frac {mv^{2}}{2}}+U} (U — потенциальная энергия)

Слева на большой объем жидкости между двумя поверхностями действует сила p1⋅S1{\displaystyle p_{1}\cdot S_{1}}, а справа — −p2⋅S2{\displaystyle -p_{2}\cdot S_{2}} (минус, потому что влево).

Итак, этот объем жидкости сдвинулся (за время dt{\displaystyle dt}). Пусть его левая граница сдвинулась на dl1{\displaystyle dl_{1}}, а правая — на dl2{\displaystyle dl_{2}}.

Пишем условие несжимаемости: S1⋅dl1=V1=V2=S2⋅dl2{\displaystyle S_{1}\cdot dl_{1}=V_{1}=V_{2}=S_{2}\cdot dl_{2}}. Объёмы, как видно, бесконечно малые, дифференциальные. Их самих можно рассматривать как дифференциалы объёма всего большого элемента.

Далее. Сначала наш большой элемент состоял из левого голубого элемента и средней синей части. Теперь он состоит из средней синей части и правого голубого элемента. При этом все его молекулы сдвинулись, но так как течение стационарное, то в каждой точке со временем энергия не меняется. Поэтому энергия средней синей части не поменялась. Поэтому работа сил (ну, или за бесконечно малое время не сама работа, а её дифференциал) равна изменению энергии, равному, в свою очередь, энергии правого голубого элементика (который добавился) минус энергия левого голубого элементика (который, наоборот, ушёл, влился в средний синий). p1⋅S1⋅dl1−p2⋅S2⋅dl2=dA=E2−E1=m2⋅v222+U2−m1⋅v122−U1=ρV2v222+U2−ρV1v122−U1{\displaystyle p_{1}\cdot S_{1}\cdot dl_{1}-p_{2}\cdot S_{2}\cdot dl_{2}=dA=E_{2}-E_{1}={\frac {m_{2}\cdot v_{2}^{2}}{2}}+U_{2}-{\frac {m_{1}\cdot v_{1}^{2}}{2}}-U_{1}={\frac {\rho V_{2}v_{2}^{2}}{2}}+U_{2}-{\frac {\rho V_{1}v_{1}^{2}}{2}}-U_{1}}.

Теперь вспоминаем формулу несжимаемости и сокращаем на объём. p1−p2=ρv222−ρv122+U2V2−U1V1{\displaystyle p_{1}-p_{2}={\frac {\rho v_{2}^{2}}{2}}-{\frac {\rho v_{1}^{2}}{2}}+{U_{2} \over V_{2}}-{U_{1} \over V_{1}}}.

Сгруппируя слагаемые, получаем формулу Бернулли: p1+U1V1+ρv122=p2+U2V2+ρv222{\displaystyle p_{1}+{U_{1} \over V_{1}}+{\frac {\rho v_{1}^{2}}{2}}=p_{2}+{U_{2} \over V_{2}}+{\frac {\rho v_{2}^{2}}{2}}}, или просто p+UV+ρv22=const{\displaystyle p+{\frac {U}{V}}+{\frac {\rho v^{2}}{2}}=const}, или, подставив потенциальную энергию, p+ρgh+ρv22=const{\displaystyle p+\rho gh+{\frac {\rho v^{2}}{2}}=const}.

Физика для средней школы

Зависимость давления жидкости от скорости ее течения

В предыдущих параграфах были рассмотрены законы равновесия жидкостей и газов. Теперь рассмотрим некоторые явления, связанные с их движением.

Движение жидкости называют течением, а совокупность частиц движущейся жидкости потоком. При описании движения жидкости определяют скорости, с которыми частицы жидкости проходят через данную точку пространства.

Если в каждой точке пространства, заполненного движущейся жидкостью, скорость не изменяется со временем, то такое движение называется установившимся, или стационарным. При стационарном течении любая частица жидкости проходит через данную точку пространства с одним и тем же значением скорости. Мы будем рассматривать только стационарное течение идеальной несжимаемой жидкости. Идеальной называют жидкость, в которой отсутствуют силы трения.

Как известно, неподвижная жидкость в сосуде, согласно закону Паскаля, передает внешнее давление ко всем точкам жидкости без изменения. Но когда жидкость течет без трения по трубе переменного поперечного сечения, давление в разных местах трубы неодинаково. Оценить распределение давлений в трубе, по которой течет жидкость, можно с помощью установки, схематически изображенной на рисунке 1. Вдоль трубы впаивают вертикальные открытые трубки-манометры. Если жидкость в трубе находится под давлением, то в манометрической трубке жидкость поднимается на некоторую высоту, зависящую от давления в данном месте трубы. Опыт показывает, что в узких местах трубы высота столбика жидкости меньше, чем в широких. Это значит, что в этих узких местах давление меньше. Чем это объясняется?

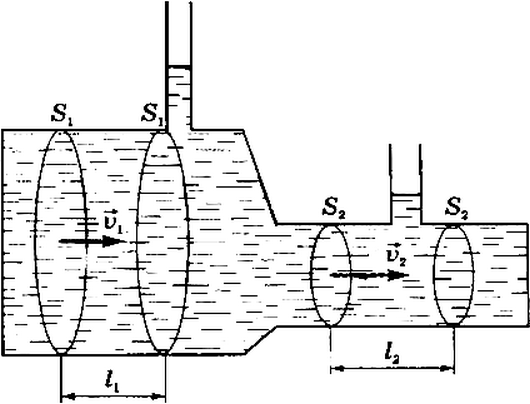
Рис. 1

Предположим, что несжимаемая жидкость течет по горизонтальной трубе с переменным сечением (рис. 1). Выделим мысленно несколько сечений в трубе, площади которых обозначим и . При стационарном течении через любое поперечное сечение трубы за равные промежутки времени переносятся одинаковые объемы жидкости.

Пусть — скорость жидкости через сечение , — скорость жидкости через сечение . За время объемы жидкостей, протекающих через эти сечения, будут равны:

Так как жидкость несжимаема, то . Следовательно, для несжимаемой жидкости. Это соотношение называется уравнением неразрывности.

Из этого уравнения , т.е. скорости жидкости в двух любых сечениях обратно пропорциональны площадям сечений. Это значит, что частицы жидкости при переходе из широкой части трубы в узкую ускоряются. Следовательно, на жидкость, поступающую в более узкую часть трубы, действует со стороны жидкости, еще находящейся в широкой части трубы, некоторая сила. Такая сила может возникнуть только за счет разности давлений в различных частях жидкости. Так как сила направлена в сторону узкой части трубы, то в широком участке трубы давление должно быть больше, чем в узком. Учитывая уравнение неразрывности, можно сделать вывод: при стационарном течении жидкости давление меньше в тех местах, где больше скорость течения, и, наоборот, больше в тех местах, где скорость течения меньше.

К этому выводу впервые пришел Д. Бернулли, поэтому данный закон называют законом Бернулли.

Применение закона сохранения энергии к потоку движущейся жидкости позволяет получить уравнение, выражающее закон Бернулли (приводим без вывода)

— уравнение Бернулли для горизонтальной трубки.

Здесь и — статические давления, — плотность жидкости. Статическое давление равно отношению силы давления одной части жидкости на другую к площади соприкосновения, когда скорость их относительного движения равна нулю. Такое давление измерил бы манометр, движущийся вместе с потоком. Неподвижная монометрическая трубка с отверстием, обращенным навстречу потоку, измерит давление

Слагаемые и имеют, с одной стороны, размерность давления, с другой — размерность объемной плотности энергии, т. е. энергии, приходящейся на единицу объема. Действительно, , масса жидкости . Если — называют динамическим давлением. Это кинетическая энергия потока в единичном объеме жидкости (объемная плотность энергии).

Если трубка не горизонтальная, то надо учитывать и гидростатическое давление жидкости. Уравнение Бернулли будет иметь вид:

где и — высоты, на которых находятся сечения и .

Закон Бернулли лежит в основе принципа действия многих технических устройств и приборов: водоструйного насоса, пульверизатора, форсунки карбюратора. Закон Бернулли позволяет объяснить возникновение подъемной силы крыла самолета.

Приборы для измерения давления.

По способу измерения дав­ления приборы разделяют на жидкостные и механические. Про­стейшим жидкостным прибором является пьезометр — пьезомет­рическая трубка, снабженная шкалой (его конструкция соответ­ствует схеме, приведенной на рис. 6.3). При известной глубине hточки присоединения пьезометра можно определить давление на поверхности :

Рис. 6.4. Жидкостные приборы для измерения давления: a — манометр; б — микроманометр; p —давление газа в сосуде; — атмосферное давление; — разность уровней жидкости; l — длина трубки, соответ­ствующая ; а — угол наклона трубки.   Давление газа р в сосуде (рис 6.4, а) можно определить с по­мощью U-образного жидкостно­го манометра: где — разность уровней жид­кости в манометре. Для определения малых зна­чений давления в сосуде исполь­зуют микроманометр (рис. 6.4, б), который    имеет наклонную труб­ку со шкалой. Вместо разности уровней  измеряют длину труб­ки l, соответствующую  , а давление находят по формуле  где a — угол наклона трубки.

В производственных условиях для измерения больших значе­ний давления применяют компактные и прочные механические манометры. Эти приборы снабжены упругими механическими эле­ментами — полыми изогнутыми пружинами или мембранами, которые деформируются при изменении давления. Перемещение упругих элементов передается стрелке, снабженной шкалой. Схе­мы таких механических маномет­ров представлены на рис. 6.5.

Рис. 6.5. Механические манометры: а — пружинный; б — мембранный; р — давление

Приборы для измерения вакуумметрического давления на­зывают вакуумметрами. По кон­струкции и принципу действия они аналогичны описанным выше приборам. На шкалу ваку­умметра нанесен знак минус, и прибор показывает отрицатель­ное давление по отношению к атмосферному. Пример. Какой силе должны противостоять болты крепления крышки люка-лаза в аппарате,

Рис. 6.6. Схема аппарата с люком-лазом, рабо­тающего под давлением: р — давление на поверхности жидкости; Р — сила, действующая на крышку; D — диаметр люка-лаза; — расстояние от центра тяжести крышки до по­верхности жидкости работающем под давлением (рис. 6.6)? Сила Р действующая на плоскую крышку, рав­на произведению давления в центре ее тяжести на площадь крышки S. С учетом формулы (6.1) где — расстояние от центра тяжести крышки до поверхности жидкости. Общая формула (6.2) упрощается в двух частных случаях:

1) если аппарат открытый, то атмосферное давление р дей­ствует на крышку как со стороны жидкости, так и снаружи. Соот­ветствующие силы уравновешивают друг друга, поэтому расчет выполняют без учета давления :

2) если давление на поверхности жидкости многократно превышает давление, создаваемое столбом жидкости (что имеет место в поршневых насосах, гидроцилиндрах объемного гидро­привода, аппаратах, работающих при высоком давлении), то силу Р определяют по формуле

Пошаговая инструкция, как рассчитать водорасход

Произвести подсчеты можно при помощи таблиц. Но полученные результаты будут неточными. Поэтому лучше проводить расчеты на месте, учитывая скорость потока, материал трубопроводных систем и прочие характеристики трубопровода.

Проще всего рассчитать объем расходуемой H2O по следующей формуле:

q=π*d2 /4*V, где:

• q – расход воды (л/с);
• V – скорость течения (м/с);
• d – диаметр (см).

Использовать эту формулу можно и для поиска других неизвестных. Если известен диаметр и расход воды, можно определить скорость потока. А если известны V и q, можно узнать диаметр.

В большинстве стояков напор водного потока равняется 1,5-2,5 атмосфер. А скорость потока обычно составляет 0,8-1,5 м/с. Может быть установлен дополнительный нагнетатель, который меняет параметры внутри системы. Все данные о нем должны быть указаны в техпаспорте.

Минимальное давление в системе должно составлять 1,5 атмосфер – этого достаточно для работы стиральной машины и посудомойки. Чем оно выше, тем быстрее вода движется по трубам, поэтому водорасход повышается.

Для получения более точных результатов применяется формула Дарси-Вейсбаха, которая учитывает возможные изменения напора воды, что приводит к повышению или снижению давления.

ΔP=λ*L/D*V2 /2q *ϸ, где:

• ΔP – потеря давления на сопротивлении движения потока;
• λ – показатель потерь на трение по всей длине;
• D – сечение трубы;
• V — скорость течения;
• L – длина трубопровода;
• g – константа = 9,8 м/с2;
• ϸ — вязкость потока.

Такую формулу обычно используют для выполнения сложных расчетов гидродинамики. В остальных случаях применяются упрощенные варианты.

Частный случай расчета водорасхода – через отверстие крана. Применяется формула:

q=S*V, где:

• Q – водорасход;
• S – площадь окружности (отверстия крана), определяется по формуле S= π*r2;
• V – скорость течения, если она неизвестна, определить ее можно, исходя из формулы V=2g*h, где g – константа, h – высота водного столба над отверстием крана.

Правила расчета

При выполнении вычислений необходимо учитывать следующие правила:

1. Следить за правильностью величин. Если одно значение исчисляется в м/с, то другое должно измеряться в л/с (не в кг/час). Иначе произведенные расчеты будут неверными.
2. Применять правильные значения констант.
3. Учитывать данные нагнетателя системы, если он используется. Вся информация о его влиянии на параметры системы указывается в техническом паспорте.
4. Промежуточные вычисления рекомендуется проводить с точными величинами, а конечный результат можно округлить (лучше в большую сторону).

Чтобы облегчить расчеты, можно воспользоваться калькуляторами в режиме онлайн, в которые достаточно только ввести все известные данные.

Когда нужно проводить вычисления?

Выполнять вычисления необходимо при выборе труб для водопровода. Диаметр должен быть подходящим, чтобы избежать чрезмерного водорасхода и обеспечить нормальный напор.

Такая необходимость появляется при проектировании дома и подведении к нему коммуникаций. При выборе трубы с оптимальным сечением для водопровода нужно обязательно выполнять ряд расчетов. Необходимо узнать максимальные объемы необходимой воды в доме за минуту.

Для этого нужно посмотреть паспортные данные стиральной и посудомоечной машин, узнать их расход. К полученным данным приплюсовать расход воды на кранах (через один прибор протекает примерно 5-6 литров за минуту времени).

Исходя из полученных результатов, нужно приобрести трубу с таким сечением, чтобы этого было достаточно для одновременной работы всех устройств и кранов.

Способы вычисления зависимостей водорасхода и диаметра трубопровода

С помощью нижеприведённых формул можно как рассчитать расход воды в трубе, так и, определить зависимость диаметра трубы от расхода воды.

В данной формуле водорасхода:

• под q принимается расход в л/с,
• V –  определяет скорость гидропотока в м/с,
• d – внутреннее сечение (диаметр в см).

Зная водорасход и d сечения, можно, применив обратные вычисления, установить скорость, или, зная расход и скорость – определить диаметр. В случае наличия дополнительного нагнетателя (например, в высотных зданиях), создаваемое им давление и скорость гидропотока указываются в паспорте прибора. Без дополнительного нагнетания скорость потока чаще всего варьируется в интервале 0,8-1,5 м/сек.

Для более точных вычислений принимают во внимание потери напора, используя формулу Дарси:

Для вычисления необходимо дополнительно установить:

• длину трубопровода (L),
• коэффициент потерь, который зависит от шероховатостей стенок трубопровода, турбулентности, кривизны и участков с запорной арматурой (λ),
• вязкость жидкости (ρ).

Зависимость между значением D трубопровода, скоростью гидропотока (V) и водорасходом (q) с учётом угла уклона (i) можно выразить в таблице, где две известные величины соединяются прямой линией, а значение искомой величины будет видно на пересечении шкалы и прямой. 

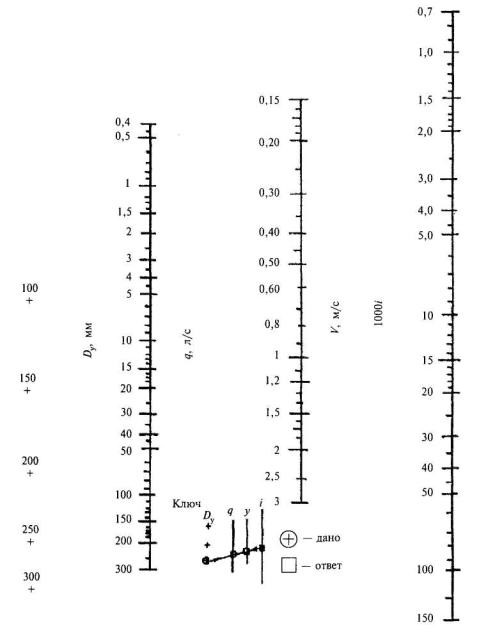
Расчёт расхода воды через трубу с учётом падения давления можно проводить с помощью онлайн-калькуляторов (например: http://allcalc.ru/node/498; https://www.calc.ru/gidravlicheskiy-raschet-truboprovoda.html). Для гидравлического расчёта, как и в формуле, нужно учесть коэффициент потерь, что предполагает выбор:

способа расчёта сопротивления,
материала и вида трубопроводных систем (сталь, чугун, асбоценмент, железобетон, пластмасса), где принимается во внимание, что, например, пластиковые поверхности менее шероховатые, чем стальные, и не подвергаются коррозии,
внутреннего диаметры,
длины участка,
падения напора на каждый метр трубопровода.

В некоторых калькуляторах учитываются дополнительные характеристики трубопроводных систем, например:

• новые или не новые с битумным покрытием или без внутреннего защитного покрытия,
• с внешним пластиковым или полимерцементным покрытием,
• с внешним цементно-песчаным покрытием, нанесённым разными методами и др.

https://youtube.com/watch?v=OWBLxN3iUgE

Читайте далее

Презентация на тему: » Гидродинамика Внутренняя и внешняя гидродинамические задачи; смешанные задачи. Основные характеристики движения жидкости. Стационарные и нестационарные.» — Транскрипт:

1

Гидродинамика Внутренняя и внешняя гидродинамические задачи; смешанные задачи. Основные характеристики движения жидкости. Стационарные и нестационарные потоки.

2

Гидродинамика Гидродинамика — раздел гидравлики, в котором изучают законы движения жидкостей. Движение или течение жидкости обусловлено разностью давлений, которое создается с помощью насосов, компрессоров, либо в следствие разности уровней или плотности жидкости. Движущаяся жидкость называется потоком жидкости.

3

Внутренняя и внешняя и смешанная гидродинамические задачи Внутренняя задача связана с движением жидкости по различным каналам и трубам. Внешняя задача посвящена обтеканию жидкостью различных тел или движению этих тел внутри жидкости. В смешанную задачу входит изучение движения жидкости по трубам или каналам при одновременном обтекании ею каких- либо тел.

4

Основные характеристики движения жидкости сечение потока (S), перпендикулярное к его оси, — живое или поперечное сечение потока; количество жидкости, протекающее в единицу времени через поперечное сечение потока, называется расходом. Расход объемный:

5

Основные характеристики движения жидкости Расход массовый: где ср — средняя скорость течения жидкости, м/с; S — поперечное сечение потока, м2; — плотность жидкости, кг/м3

6

Основные характеристики движения жидкости Гидравлический радиус: Эквивалентный диаметр:

7

Режимы движения жидкости а – ламинарный; в – турбулентный:

8

Критерий Рейнольдса Критерий Re является мерой соотношения между силами вязкости и инерции в движущемся потоке.

9

Критерий Рейнольдса Установлено, что переход ламинарного движения в турбулентное происходит при значениях критерия Рейнольдса выше критического. Для круглых трубок Re кр =2320. При Re>Re кр — турбулентный режим течения, при Re2320, но Re устойчивый турбулентный.

10

Распределение скоростей в потоке

11

Гидродинамический пограничный слой При турбулентном движении у стенок трубопровода имеется тонкий слой жидкости, движущийся в ламинарном режиме, т.к. силы вязкости оказывают превалирующее влияние на движение жидкости. Ламинарный слой и переходная зона – гидродинамический пограничный слой.

12

Оптимальный диаметр трубопроводов При определении диаметров трубопроводов нужно знать секундный расход жидкости и среднюю скорость ее движения:

13

Средняя скорость движения жидкости Капельные жидкости 1-3 м/с ; Газ под небольшим давлением 8-15 м/с; Газ под большим давлением м/с; Насыщенный водяной пар м/с; Перегретый водяной пар м/с

Термодинамика закона Бернулли

Из статистической физики следует, что на линиях тока при адиабатическом течении остается постоянным следующее соотношение:

v22+w+φ=const,{\displaystyle {\frac {v^{2}}{2}}+w+\varphi =\mathrm {const} ,}

где w{\displaystyle w} — энтальпия единицы массы, φ{\displaystyle \varphi } — потенциал силы.

Вывод закона Бернулли из уравнения Эйлера и термодинамических соотношений

1. Запишем Уравнение Эйлера:

ρ∂v→∂t+ρ(v→,∇)v→=−∇p−ρ∇φ{\displaystyle \rho {\frac {\partial {\vec {v}}}{\partial t}}+\rho ({\vec {v}},\nabla ){\vec {v}}=-\nabla p-\rho \nabla \varphi }

φ{\displaystyle \varphi } — потенциал. Для силы тяжести φ=gz{\displaystyle \varphi =gz}

2. Запишем выражение для энтальпии и предположим, что энтропия системы постоянна (или, можно сказать, что течение адиабатично):

dW=VdP+TdS{\displaystyle dW=VdP+TdS}

Пусть S=const{\displaystyle S=const} и w{\displaystyle w} — энтальпия единицы массы, тогда:

dw=dpρ{\displaystyle dw={\frac {dp}{\rho }}}

или

∇w=∇pρ{\displaystyle \nabla w={\frac {\nabla p}{\rho }}}

3. Воспользуемся следующими соотношениями из векторной алгебры:

12∇v2=(v→,∇)v→+v→×rot⁡v→{\displaystyle {\frac {1}{2}}\nabla v^{2}=({\vec {v}},\nabla ){\vec {v}}+{\vec {v}}\times \operatorname {rot} {\vec {v}}}

l→⋅∇=∂∂l{\displaystyle {\vec {l}}\cdot \nabla ={\frac {\partial }{\partial l}}} — проекция градиента на некоторое направление равно производной по этому направлению.

4. Уравнение Эйлера с использованием соотношений выведенных выше:

ρ∂v→∂t+ρ12∇v2−v→×rot⁡v→=−ρ∇(φ+w){\displaystyle \rho {\frac {\partial {\vec {v}}}{\partial t}}+\rho \left=-\rho \nabla (\varphi +w)}

Спроецируем это уравнение на единичный вектор касательный к линии тока, учитывая следующее:

∂v→∂t={\displaystyle {\frac {\partial {\vec {v}}}{\partial t}}=0} — условие стационарности

(l→,v→×rot⁡v→)={\displaystyle ({\vec {l}},{\vec {v}}\times \operatorname {rot} {\vec {v}})=0} — так как l→||v→{\displaystyle {\vec {l}}||{\vec {v}}}

Получаем:

∂∂l(v22+w+φ)={\displaystyle {\frac {\partial }{\partial l}}\left({\frac {v^{2}}{2}}+w+\varphi \right)=0}

То есть на линиях тока в стационарной адиабатической жидкости выполняется следующее соотношение:

v22+w+φ=const{\displaystyle {\frac {v^{2}}{2}}+w+\varphi =\operatorname {const} }

Уравнение Бернулли

Подробности

Категория: Гидравлика

Документальные учебные фильмы. Серия «Физика».

 Даниил Бернулли (Daniel Bernoulli; 29 января (8 февраля) 1700 — 17 марта 1782), швейцарский физик-универсал, механик и математик, один из создателей кинетической теории газов, гидродинамики и математической физики. Академик и иностранный почётный член (1733) Петербургской академии наук, член Академий: Болонской (1724), Берлинской (1747), Парижской (1748), Лондонского королевского общества (1750). Сын Иоганна Бернулли.

https://vk.com/video_ext.php

Закон (уравнение) Бернулли является (в простейших случаях) следствием закона сохранения энергии для стационарного потока идеальной (то есть без внутреннего трения) несжимаемой жидкости:

Здесь

 — плотность жидкости,

 — скорость потока,

 — высота, на которой находится рассматриваемый элемент жидкости,

 — давление в точке пространства, где расположен центр массы рассматриваемого элемента жидкости,

 — ускорение свободного падения.

Уравнение Бернулли также может быть выведено как следствие уравнения Эйлера, выражающего баланс импульса для движущейся жидкости.

В научной литературе закон Бернулли, как правило, называется уравнением Бернулли(не следует путать с дифференциальным уравнением Бернулли), теоремой Бернулли или интегралом Бернулли.

Константа в правой части часто называется полным давлением и зависит, в общем случае, от линии тока.

Размерность всех слагаемых — единица энергии, приходящаяся на единицу объёма жидкости. Первое и второе слагаемое в интеграле Бернулли имеют смысл кинетической и потенциальной энергии, приходящейся на единицу объёма жидкости

Следует обратить внимание на то, что третье слагаемое по своему происхождению является работой сил давления и не представляет собой запаса какого-либо специального вида энергии («энергии давления»)

Соотношение, близкое к приведенному выше, было получено в 1738 г. Даниилом Бернулли, с именем которого обычно связывают интеграл Бернулли. В современном виде интеграл был получен Иоганном Бернулли около 1740 года.

Для горизонтальной трубы высота постоянна и уравнение Бернулли принимает вид:   .

Эта форма уравнения Бернулли может быть получена путём интегрирования уравнения Эйлера для стационарного одномерного потока жидкости, при постоянной плотности :   .

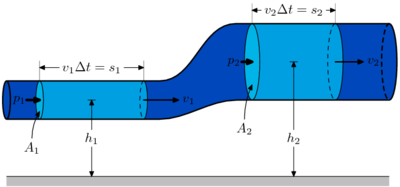
Согласно закону Бернулли, полное давление в установившемся потоке жидкости остается постоянным вдоль этого потока.

Полное давление состоит из весового , статического и динамического давлений.

Из закона Бернулли следует, что при уменьшении сечения потока, из-за возрастания скорости, то есть динамического давления, статическое давление падает. Это является основной причиной эффекта Магнуса. Закон Бернулли справедлив и для ламинарных потоков газа. Явление понижения давления при увеличении скорости потока лежит в основе работы различного рода расходомеров (например труба Вентури), водо- и пароструйных насосов. А последовательное применение закона Бернулли привело к появлению технической гидромеханической дисциплины — гидравлики.

Закон Бернулли справедлив в чистом виде только для жидкостей, вязкость которых равна нулю. Для приближённого описания течений реальных жидкостей в технической гидромеханике (гидравлике) используют интеграл Бернулли с добавлением слагаемых, учитывающих потери на местных и распределенных сопротивлениях.

Известны обобщения интеграла Бернулли для некоторых классов течений вязкой жидкости (например, для плоскопараллельных течений), в магнитной гидродинамике, феррогидродинамике.

В статье были спользованны материалы Wikipedia

Презентация на тему: » Тема 9 гидродинамика. 2 способа описания движения движение частиц или малых объемов жидкости (метод Лагранжа) свойства жидкости в каждой точке пространства.» — Транскрипт:

1

Тема 9 гидродинамика

2

2 способа описания движения движение частиц или малых объемов жидкости (метод Лагранжа) свойства жидкости в каждой точке пространства (метод Эйлера)

3

2 вида течений Если течение плавное и смежные слои как бы скользят друг относительно друга, то его называют ламинарным или слоистым. В этом случае каждая частица жидкости движется по гладкой траектории и траектории разных частиц не пересекаются. Когда скорость течения превышает определенный предел, зависящий от ряда факторов, течение становится турбулентным. Турбулентное течение характеризуется наличием беспорядочных маленьких водоворотов, называемых вихрями. Вихри поглощают огромное количество энергии.

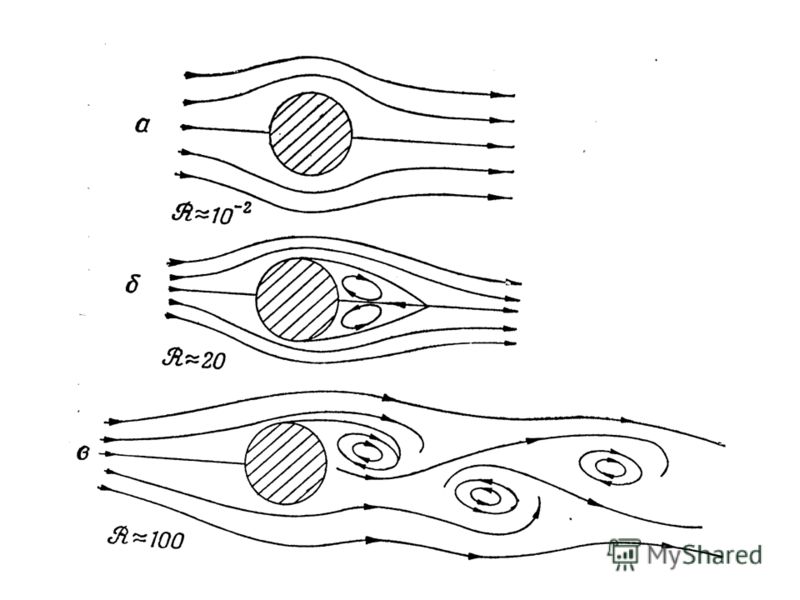
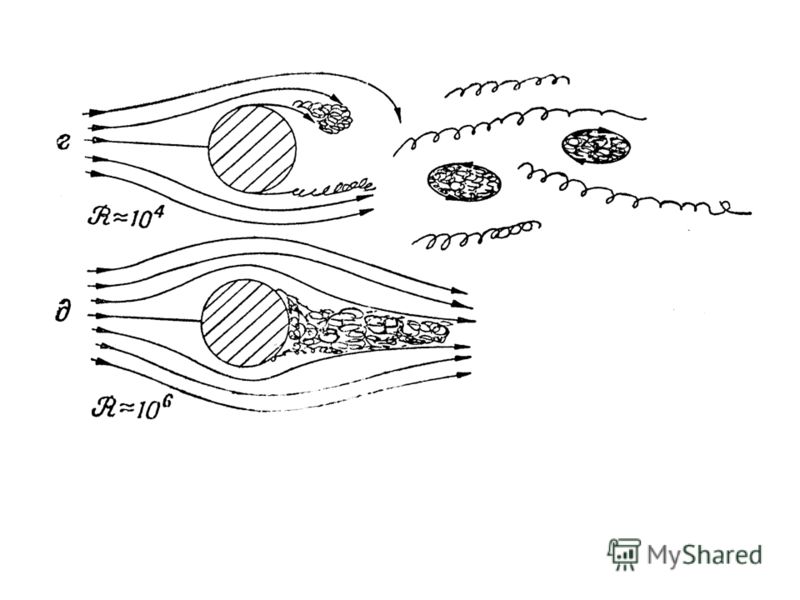
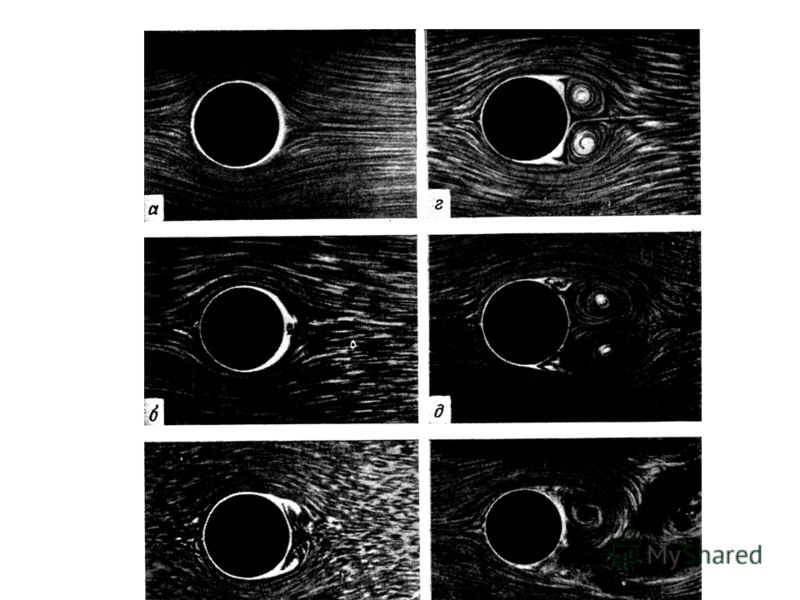
8

4 важнейшие характеристики жидкость (газ) сжимаемая или несжимаемая жидкость вязкая или невязкая (идеальная) течение установившееся (стационарное) или нестационарное течение вихревое или безвихревое (потенциальное) В безвихревой жидкости полный момент импульса относительно любой точки равен нулю. можно проверить маленькой вертушкой

9

Уравнение неразрывности В ламинарном потоке траектория движения частицы называется линией тока. Скорость в любой точке направлено по касательной к линии тока. Линии тока не пересекаются, так как иначе скорость не однозначна. Пучок линий тока называется трубкой тока.

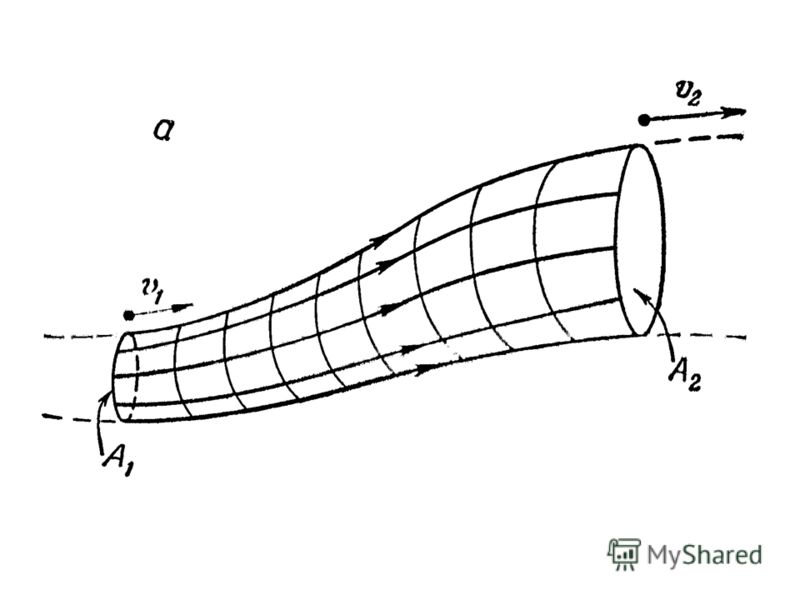
11

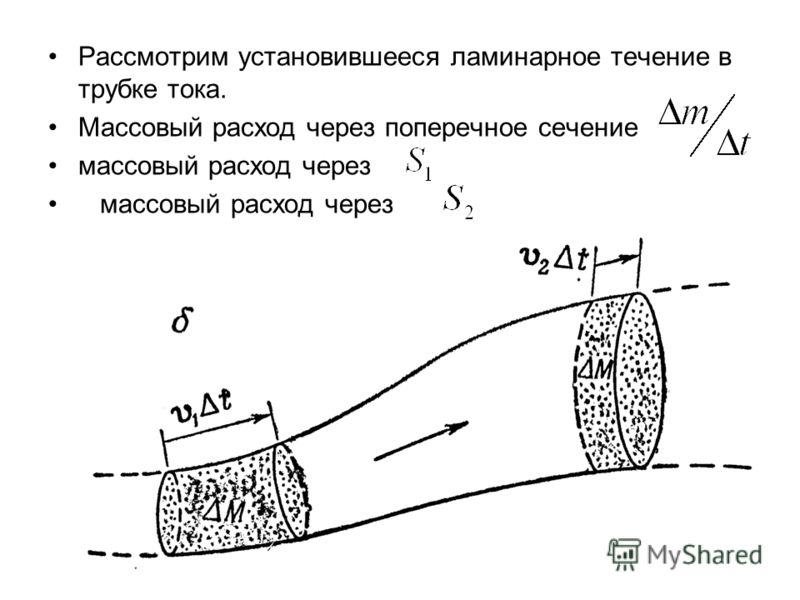
Рассмотрим установившееся ламинарное течение в трубке тока. Массовый расход через поперечное сечение массовый расход через

12

Так как расход через стенки трубки тока отсутствует уравнение неразрывности Если жидкость несжимаемая

13

Вязкость (внутреннее трение) Вязкость можно представить себе как трение при движении слоев среды относительно друг друга. В жидкости вязкость обусловлена силами когезии между молекулами, а в газах – столкновениями атомов и молекул. Количественным выражением вязкости является коэффициент вязкости (эта)

14

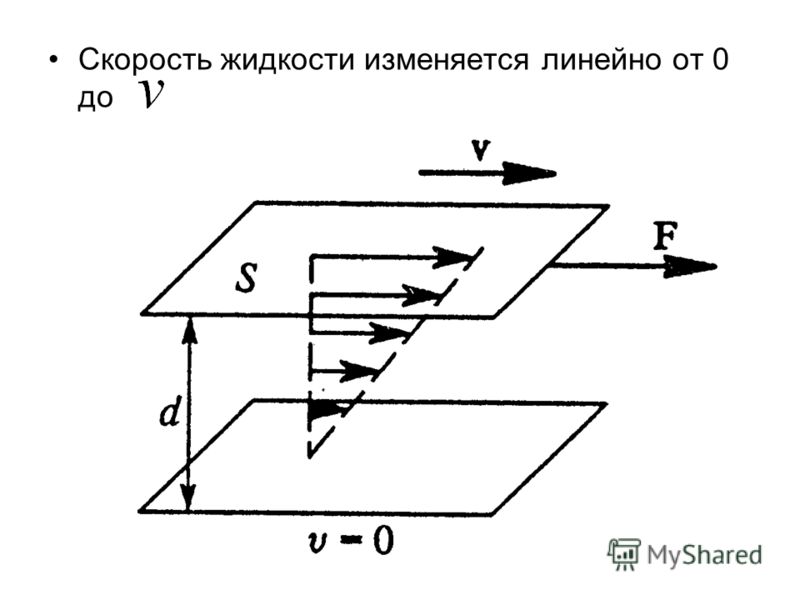
Скорость жидкости изменяется линейно от 0 до

15

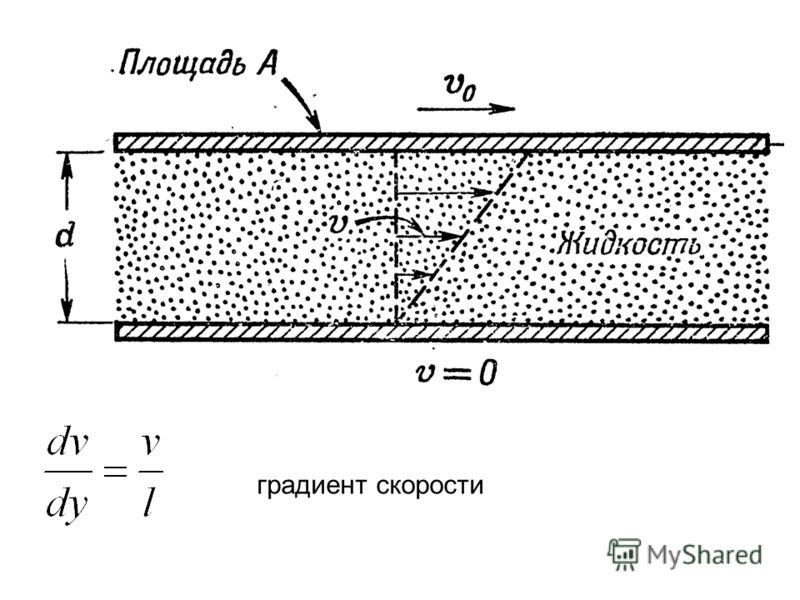
градиент скорости

16

Для любой жидкости (опыт) зависит от температуры. В общем случае формула справедлива для ньютоновских жидкостей Кровь – неньютоновская жидкость

17

Вывод формулы вязкого трения для газа Рассмотрим перенос импульса при переходе из слоя в слой. Перемешивание молекул разных слоев, происходящих в силу хаотического движения приводит к выравниванию скоростей переносного движения разных слоев, что проявляется макроскопически как действие сил трения между слоями.

18

но переносят разное количество движения

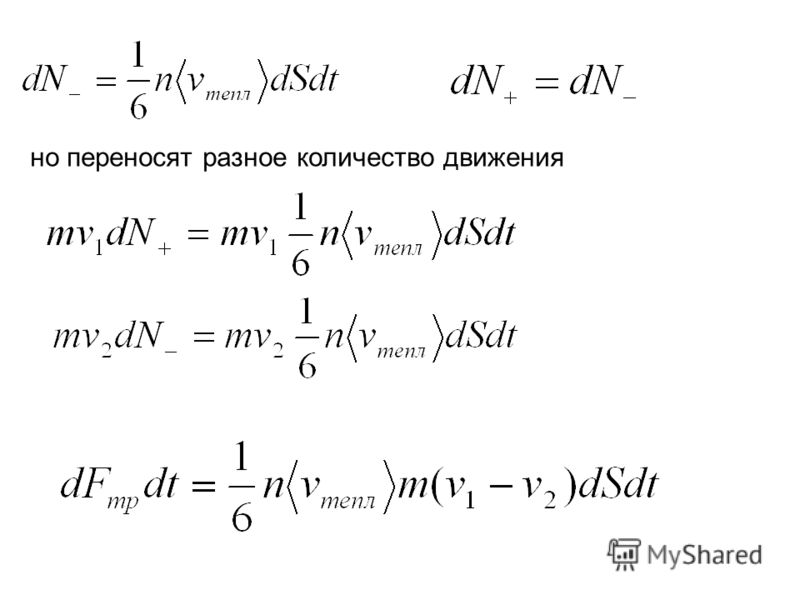
19

Коэффициент вязкости численно равен силе внутреннего трения, действующей на единицу площади границы раздела параллельно движущихся слоев газа, когда скорость их движения уменьшается на единицу при перемещении в направлении, перпендикулярном к границе, на единицу длины.

20

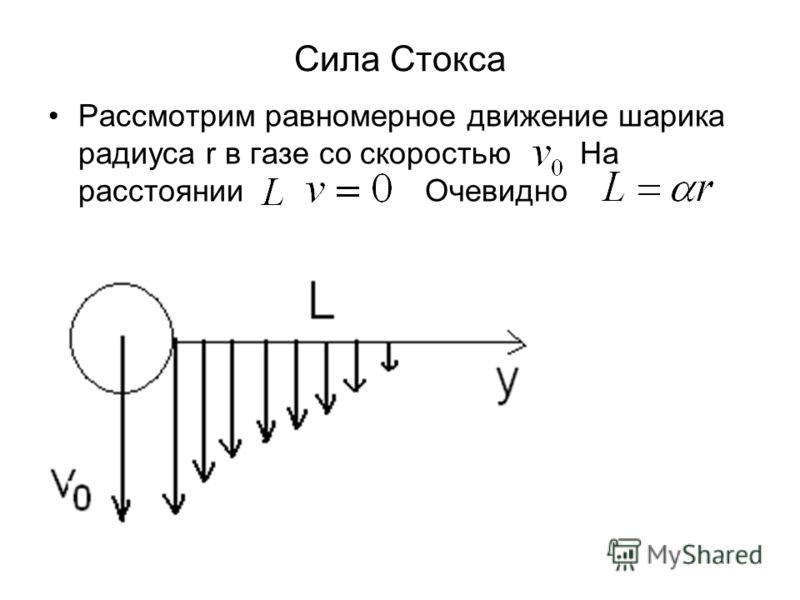
Сила Стокса Рассмотрим равномерное движение шарика радиуса r в газе со скоростью На расстоянии Очевидно

21

поверхность шарика Стокс

22

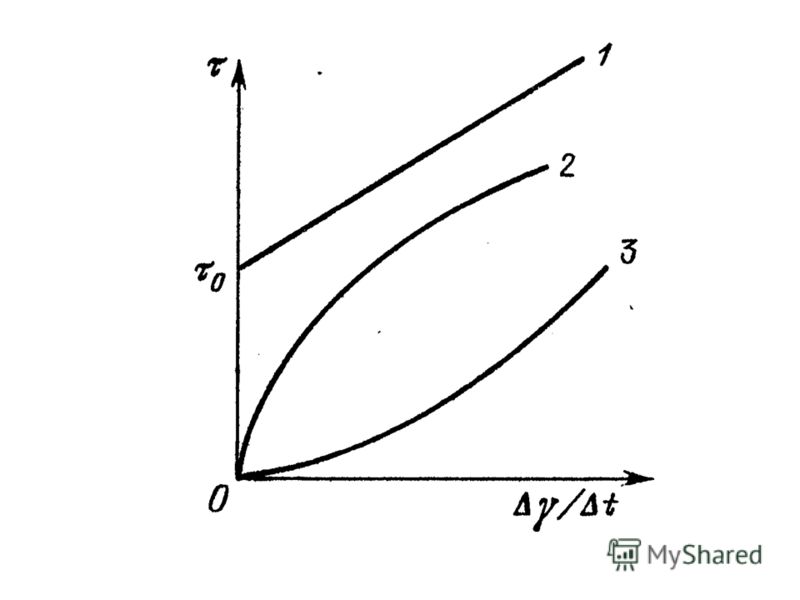
Для несферических тел зависит от формы и ориентации. Для больших тел По скорости падения можно определить

24

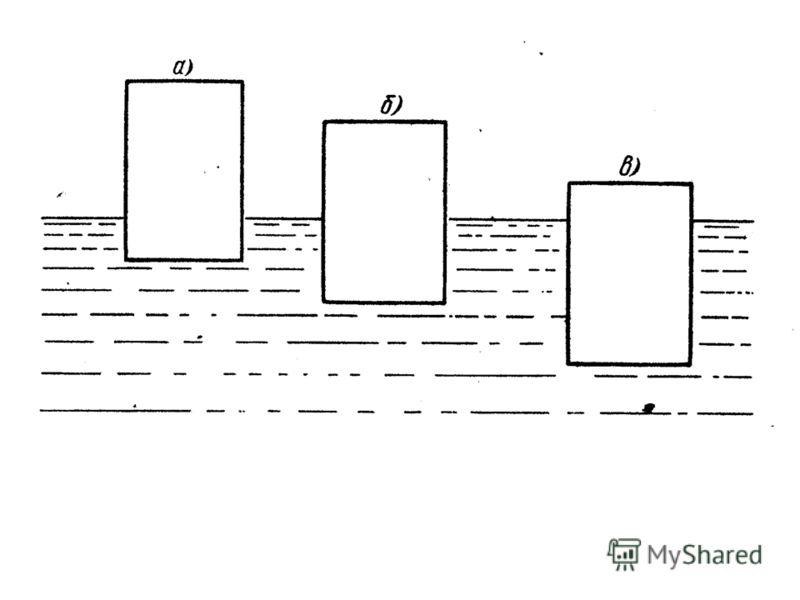
Бингамовская жидкость Реологические кривые Бингамовские жидкости это такие вещества, которые при малых напряжений не текут. До тех пор пока сдвиговое напряжение не превысит критического значения, бингамовская жидкость сопротивляется сдвигу как твердое тело. Но как только превысит предел текучести – бингамовская жидкость потечет как обычная ньютоновская жидкость.

26

Число Рейнольдса

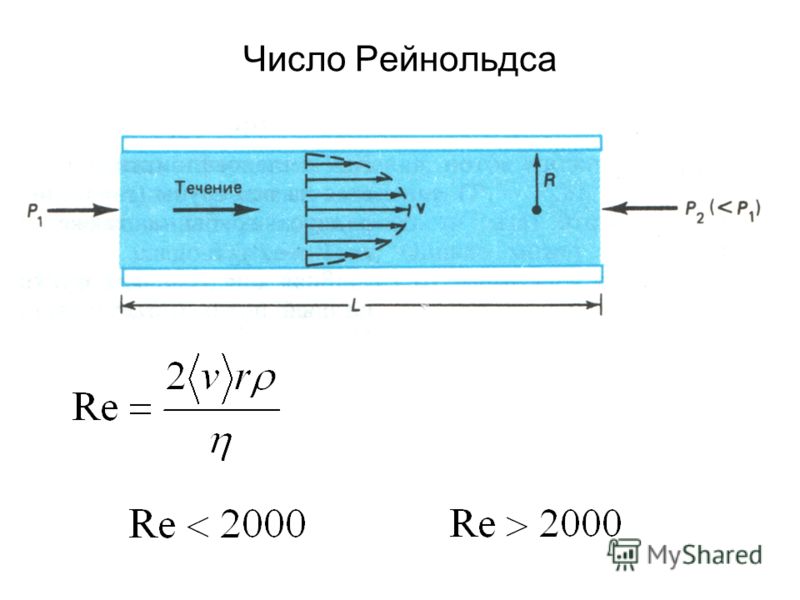
ФизикаУчебник для 10 класса

§ 9.10. Давление в движущихся жидкостях и газах

При изучении гидростатики мы выясняли, как распределяется давление в неподвижной жидкости (см. § 9.5). Теперь познакомимся с распределением давления в движущейся жидкости.

Вначале обратимся к опытным фактам. Возьмем трубку переменного сечения с небольшими отверстиями в стенке, в которые вставлены стеклянные открытые сверху измерительные трубки (рис. 9.39). При стационарном течении жидкость в каждой измерительной трубке поднимается до определенной высоты (высоты необходимо отсчитывать от какого-либо горизонтального уровня).

Рис. 9.39

По высоте столба жидкости в измерительных трубках можно судить о ее давлении на стенки горизонтальной трубки. Опыт показывает, что в широких местах трубки давление больше, чем в узких. Но чем больше сечение трубки, тем меньше скорость течения жидкости (см. § 9.9). Следовательно, можно сделать вывод:

При стационарном течении жидкости давление больше в тех местах, где меньше скорость течения, и, наоборот, меньше в тех местах, где скорость течения больше.

Эта зависимость была установлена Д. Бернулли(1).

Факт уменьшения давления с увеличением скорости жидкости на первый взгляд кажется парадоксальным. Казалось бы, что при переходе из широкой части трубки в узкую жидкость должна сжиматься, поэтому давление внутри нее и на стенки трубки должно возрастать. В действительности же все происходит наоборот. Сначала попытаемся объяснить это явление качественно на основе второго закона Ньютона и условия неразрывности стационарного потока жидкости, считая жидкость идеальной.

Выделим элемент жидкости, который движется вдоль оси трубки. При переходе из широкой части трубки в узкую скорость течения увеличивается, поэтому ускорение выделенного элемента жидкости направлено по течению, а при переходе из узкой части в широкую — против течения. Согласно второму закону Ньютона ускорение вызывается силой и совпадает с ней по направлению. Такой силой может быть лишь равнодействующая сил давления окружающей жидкости на поверхность выделенного объема. Значит, давление на элемент жидкости при переходе его из широкой части трубки в узкую должно быть больше со стороны жидкости в широкой части трубки, чем со стороны узкой (рис. 9.40). При переходе же элемента из узкой части трубки в широкую ускорение направлено против течения. В эту же сторону должна быть направлена равнодействующая сил давления, что опять-таки возможно, если давление жидкости со стороны широкой части трубки больше, чем со стороны узкой.

Рис. 9.40

Чем быстрее движется жидкость, тем меньше давление внутри нее.

(1) Бернулли Даниил (1700—1782) — швейцарский физик, академик Петербургской академии наук с 1725 по 1733 г., а позже — ее иностранный почетный член.